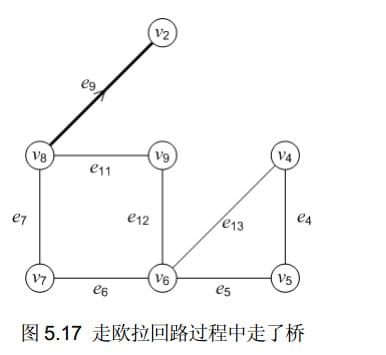
有关双向BFS的一次尝试
什么是双向BFS
双向BFS在寒假解决图论中搜索问题时就已经遇到了,单向BFS是从一个起点到一个终点搜索,找最短路,而双向BFS是不仅从起点到终点搜索,而且同时从终点出发,向起点进行搜索。双向BFS看起来能快很多。
当时和龙哥讨论,感觉双向BFS理论上不会快到哪去,毕竟搜索就是枚举的过程,加上当时我还不会双向BFS,就没有细究。
双向BFS为什么快
昨天开始学双向BFS并拿了一个题进行试验,发现双向BFS的确快(有图有真相):

第一次提交(11:46)是用普通的BFS写的,然后在普通的BFS基础上改为了双向BFS然后提交发现确实快了。
双向BFS为什么快本身就是个很奇妙的问题,有两张图也许能很好的说明问题:

单向BFS(上图)
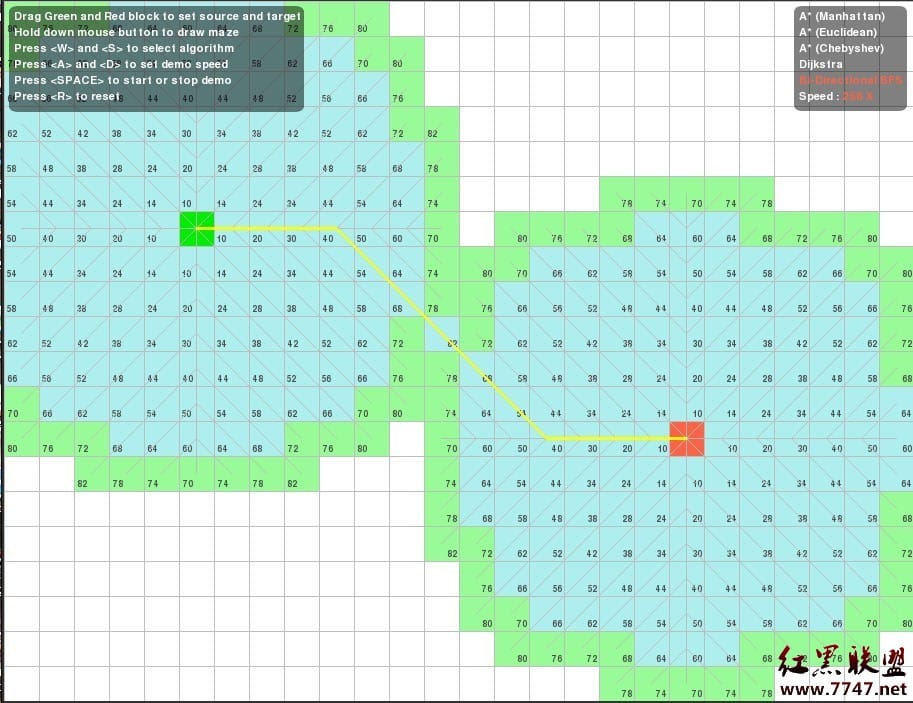
双向BFS(上图)
(图出自:红黑联盟)
如果把搜索看成一个圆,那么圆的面积可以看做能表示搜索次数的一个值。而起点s和终点e之间的距离可以大体看为园的半径。
对于单向BFS(第一个图)来说,假设路径为L,那么搜索次数为 LLPI(PI为圆周率)。
对于双向BFS(第二个图)来说,假设路径为L,那么搜索次数为2*(L/2)*(L/2)*PI。
相比较来说,的确可以节省很多时间,而能节省多少是根据图的大小和L的大小来决定的,图越大,L越小,节省时间越明显。
双向BFS怎么实现
双向BFS有好几种实现,我只说我自己用的这种。
先贴出HDU1195题的单向BFS和双向BFS代码,不同之处显而易见:
单向:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct Node
{
int num;
int t;
};
int bj[10000];
void fen(int num[4],int n)
{
num[0] = n / 1000;
num[1] = (n / 100) % 10;
num[2] = (n / 10) % 10;
num[3] = n % 10;
}
int he(int num[4])
{
int sum = 0;
for(int i = 0;i < 4;i++)
sum = sum * 10 + num[i];
return sum;
}
int bfs(int s,int e)
{
queue<Node> que;
while(!que.empty())
que.pop();
Node now,tmp;
now.num = s;
now.t = 0;
que.push(now);
bj[now.num] = 1;
while(!que.empty())
{
now = que.front();
que.pop();
if(now.num == e)
return now.t;
int tn[4];
//枚举每一位
for(int i = 0;i < 4;i++)
{
//加一
fen(tn,now.num);
tn[i] += 1;
if(tn[i] == 10)
tn[i] = 1;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = 1;
que.push(tmp);
}
//减一
fen(tn,now.num);
tn[i] -= 1;
if(tn[i] == 0)
tn[i] = 9;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = 1;
que.push(tmp);
}
}
//交换相邻两个数位置
for(int i = 0;i < 3;i++)
{
fen(tn,now.num);
tn[i] ^= tn[i + 1];
tn[i + 1] ^= tn[i];
tn[i] ^= tn[i + 1];
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = 1;
que.push(tmp);
}
}
}
return -1;
}
int main()
{
int N;
cin >> N;
while(N--)
{
int num1,num2;
memset(bj,0,sizeof(bj));
cin >> num1 >> num2;
int ans = bfs(num1,num2);
cout << ans << endl;
}
}
双向:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct Node
{
int num;
int t;
};
int bj[10000];
int ti[10000];
void fen(int num[4],int n)
{
num[0] = n / 1000;
num[1] = (n / 100) % 10;
num[2] = (n / 10) % 10;
num[3] = n % 10;
}
int he(int num[4])
{
int sum = 0;
for(int i = 0;i < 4;i++)
sum = sum * 10 + num[i];
return sum;
}
int bfs(int s,int e)
{
queue<Node> que;
while(!que.empty())
que.pop();
Node now,tmp;
now.num = s;
now.t = 0;
que.push(now);
bj[now.num] = 1;
now.num = e;
now.t = 0;
que.push(now);
bj[now.num] = 2;
while(!que.empty())
{
now = que.front();
que.pop();
int tn[4];
//枚举每一位
for(int i = 0;i < 4;i++)
{
//加一
fen(tn,now.num);
tn[i] += 1;
if(tn[i] == 10)
tn[i] = 1;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = bj[now.num];
ti[tmp.num] = tmp.t;
que.push(tmp);
}else if(bj[tmp.num] != bj[now.num])
{
return ti[tmp.num] + ti[now.num] + 1;
}
//减一
fen(tn,now.num);
tn[i] -= 1;
if(tn[i] == 0)
tn[i] = 9;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = bj[now.num];
ti[tmp.num] = tmp.t;
que.push(tmp);
}else if(bj[tmp.num] != bj[now.num])
{
return ti[tmp.num] + ti[now.num] + 1;
}
}
//交换相邻两个数位置
for(int i = 0;i < 3;i++)
{
fen(tn,now.num);
tn[i] ^= tn[i + 1];
tn[i + 1] ^= tn[i];
tn[i] ^= tn[i + 1];
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = bj[now.num];
ti[tmp.num] = tmp.t;
que.push(tmp);
}else if(bj[tmp.num] != bj[now.num])
{
return ti[tmp.num] + ti[now.num] + 1;
}
}
}
return -1;
}
int main()
{
int N;
cin >> N;
while(N--)
{
int num1,num2;
memset(bj,0,sizeof(bj));
cin >> num1 >> num2;
int ans = bfs(num1,num2);
cout << ans << endl;
}
}
两份代码一共有两大区别,一个是标记数组,一个是记录到当前位置的距离数组。
第一个大区别就是标记,单向BFS的标记很单纯,就是标记有没有走过,而双向BFS不仅标记有没有走过,还进行区分标记,来记录到底是从起点走到当前点的还是从终点走到当前点的。也可以认为这是不同的两层搜索同时进行,分别标记。如果两层标记相遇,就认为已经找到了一条路径连通了起点和终点。
第二大区别就是距离数组,单向BFS不需要这个数组因为队列里的t变量就足够记录到当前位置的最短路(如果当前位置为终点,这个最短路就是答案)。而双向这个t的含义是从起点到当前位置的最短距离,因为有两个起点,所以不能记录两条路径(不同起点)的路径和,因此需要一个距离数组保存不同路径到当前位置的距离,当两条路径相接之后,只需要将保存接触点的距离相加便是答案。
DFS(深度优先搜索)的非递归实现
突然想起来搜索是属于图论的,那么在解决图论的过程中把搜索解决掉。没想到非递归实现一下就搞了两天。虽然有些疑问还没有解决,但感觉已经可以写总结了,与其说总结,不如说一次尝试的记录(因为有个题最后还是TLE嘛)。(求规范代码!!!@啸爷)
众所周知,DFS的常规写法是递归实现,但递归普遍慢所以可以用模拟递归栈来循环实现。这样做有两个好处,一个是循环实现要比递归实现更快,第二个是因为模拟的栈是在程序中手动开的存储空间而不是通过递归用的计算机本身的栈,相当于外挂栈,在数量巨大的DFS的过程中不会爆栈。
当然,这是传统这么认为的,第二点没什么好说的,全局变量开的数组的确可以比递归用的栈大,所以更能有效的防止爆栈。但是关于第一点,我觉得还是有待考虑的。原因是我写的两种DFS非递归实现一个超时,一个和递归实现用时一样= =。我现在还不认为是我的代码有问题,如果大家发现问题请留言,感激不尽。
先说那个和递归实现一样的那个。
因为DFS基本上就分两种,一种是以遍历全图为目的的,需要边走边标记,而回退之后不用清除标记。目的是遍历全图嘛,标记正记录了走过的位置而方便找没有走过的位置。一种以搜索路径为目的,最短路也好,恰好到达也好,找的是一条路径问题,而最大的区别就是如果发生退栈,要进行清除标记,因为退栈后,可能存在别的路径依然会访问到这个结点。
这种DFS以POJ1562为例:
先看效果,我第一次提交是用DFS的递归实现,第二次是用非递归实现,虽然两个用时一样,但是我们还是能确定非递归实现不一定要比递归慢(我只能精确到这了TAT,我目前还没遇到递归TLE,非递归过的题目,但的确遇到了非递归TLE,递归过的题目= =)。

递归代码:
#include <iostream>
#include <cstring>
using namespace std;
char mp[150][150];
int chx[] = {1,0,-1,0,1,-1,1,-1};
int chy[] = {0,1,0,-1,1,-1,-1,1};
bool bj[150][150];
void dfs(int x,int y,int n,int m)
{
for(int i = 0;i < 8;i++)
{
int tx = x + chx[i];
int ty = y + chy[i];
if(tx >= 0 && ty >= 0 && tx < n && ty < m)
{
if(bj[tx][ty] == 0)
{
bj[tx][ty] = 1;
if(mp[tx][ty] == '@')
{
dfs(tx,ty,n,m);
}
}
}
}
}
int main()
{
int n,m;
while(cin >> n >> m,n)
{
memset(bj,0,sizeof(bj));
for(int i = 0;i < n;i++)
cin >> mp[i];
int ans = 0;
for(int i = 0;i < n;i++)
{
for(int j = 0;j < m;j++)
{
if(bj[i][j] == 0 && mp[i][j] == '@')
{
dfs(i,j,n,m);
ans++;
}
}
}
cout << ans << endl;
}
return 0;
}
很常规的写法,我们根据题目要求,找到‘@’就向下搜索,直到把相连的@全部标记完成,统计有几块不相连的@。
其中遇到相连的@便进入递归直到没有找到@再回退,换一个方向继续向下搜索。
而非递归实现就是模拟这个过程:
#include <iostream>
#include <cstring>
using namespace std;
struct Stack
{
int x,y;
}s[100000];
char mp[150][150];
int chx[] = {1,0,-1,0,1,-1,1,-1};
int chy[] = {0,1,0,-1,1,-1,-1,1};
bool bj[150][150];
void dfs(int x,int y,int n,int m)
{
int t = 0;
Stack now,tmp;
now.x = x;
now.y = y;
s[t++] = now;
bj[x][y] = 1;
while(t > 0)
{
now = s[t - 1];
int flag = 0;
for(int i = 0;i < 8;i++)
{
tmp.x = now.x + chx[i];
tmp.y = now.y + chy[i];
if(tmp.x >= 0 && tmp.y >= 0 && tmp.x < n && tmp.y < m)
{
if(bj[tmp.x][tmp.y] == 0)
{
bj[tmp.x][tmp.y] = 1;
if(mp[tmp.x][tmp.y] == '@')
{
s[t++] = tmp;
flag = 1;
break;
}
}
}
}
if(flag)
continue;
t--;
}
}
int main()
{
int n,m;
while(cin >> n >> m,n)
{
memset(bj,0,sizeof(bj));
for(int i = 0;i < n;i++)
cin >> mp[i];
int ans = 0;
for(int i = 0;i < n;i++)
{
for(int j = 0;j < m;j++)
{
if(bj[i][j] == 0 && mp[i][j] == '@')
{
dfs(i,j,n,m);
ans++;
}
}
}
cout << ans << endl;
}
return 0;
}
我们手动创建了一个栈,如果找到‘@’就更新栈顶,然后跳出各个方向的向下遍历,因为如果不跳出,就成以这个点为起点向周围各个方向搜索的类似BFS的东西了。
更新栈顶之后便以栈顶为起点继续向下搜索,但是如果向下没有找到‘@’,也就是说没法继续更新栈顶,那只能做回退处理。但是这里有个问题,当然在这种类型的DFS中并不是问题,但是再第二个类型的DFS中需要特殊处理,那就是在递归中我们可以很好实现当回退之后,换个方向继续搜索,因为刚才的路径、方向都已经在递归栈中保存了,相当于挂起,但循环模拟却没有对之前的状态进行保存处理,举个例子:从A以第1个方向走到B(并作标记),在B没有找到下路,需要回退到A,然后A重新成为栈顶继续向下遍历,理论上应该是从第2个方向继续遍历,而循环实现依旧是从第1个方向开始,原因很好理解。至于怎么改善,讲第二种DFS的时候再做叙述。
第二种DFS,以搜索路径为目的,最短路也好,恰好到达也好,找的是一条路径问题,而最大的区别就是如果发生退栈,要进行清除标记,因为退栈后,可能存在别的路径依然会访问到这个结点。我们以ZOJ2110为例,我昨天这个题卡了一下午,递归实现很顺利就A掉了,但是非递归实现到现在还是TLE,十分费解(坏了,留下阴影了,再也不会爱了TAT)。
还是先看交题记录
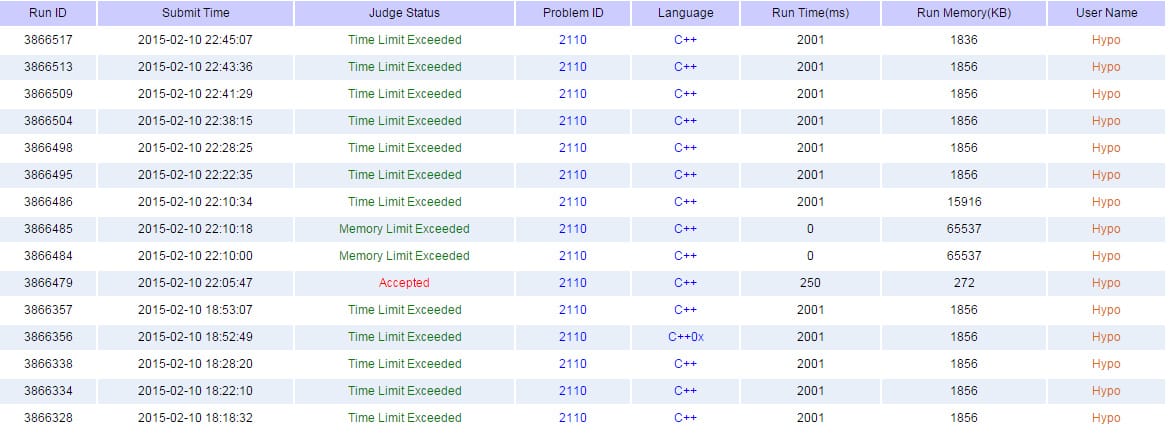
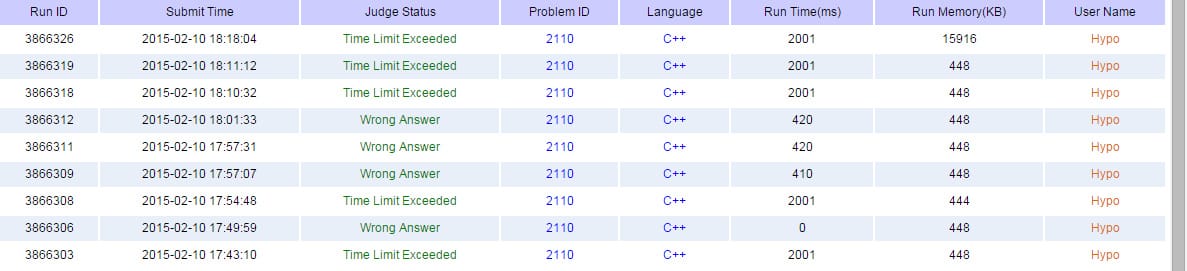
因为第一次写这种类型的DFS,开始的那几个WA大家请忽视= =。
其中有个AC是我实在怀疑非递归了(一开始就是用非递归写的),然后用递归写了一下,一下就A掉了,简直醉了。
这个题目需要剪枝,其实就是深度优先搜索(DFS)的奇偶剪枝那篇文章的例题,如果想看递归实现和剪枝优化,请左转那篇之前写的文章,下面只说非递归实现。代码:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <math.h>
using namespace std;
char map_[10][10];
bool bj[10][10];
int chx[] = {0,1,0,-1};
int chy[] = {1,0,-1,0};
struct Stack
{
int x,y,t;
int n;
} s[100000];
int main()
{
int n,m,tim;
while(cin >> n >> m >> tim,n)
{
for(int i = 0; i < n; i++)
{
cin >> map_[i];
}
int x = -1,y = -1;
int fx = -1,fy = -1;
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
if(map_[i][j] == 'S')
{
x = i;
y = j;
}
if(map_[i][j] == 'D')
{
fx = i;
fy = j;
}
}
}
if(x == -1 || fx == -1)
{
cout << "NO" << endl;
continue;
}
memset(bj,0,sizeof(bj));
int t = 0;
s[t].x = x;
s[t].y = y;
s[t].t = 0;
s[t].n = 0;
t++;
bj[x][y] = 1;
bool flag = 1;
Stack tmp,now;
while(t > 0)
{
now = s[t - 1];
if(now.x == fx && now.y == fy)
{
if(now.t == tim)
{
cout << "YES" << endl;
flag = 0;
break;
}
}
int pdtmp = tim - now.t - fabs(fx - now.x) - fabs(fy - now.y);
if(pdtmp < 0 || pdtmp % 2)
{
t--;
if(t == 0)
break;
s[t - 1].n++;
bj[s[t].x][s[t].y] = 0;
continue;
}
int tf = 0;
for(int i = now.n; i < 4; i++)
{
tmp.x = now.x + chx[i];
tmp.y = now.y + chy[i];
tmp.t = now.t + 1;
tmp.n = 0;
now.n = i;
if(tmp.x >= 0 && tmp.y >= 0 && tmp.x < n && tmp.y < m)
{
if(map_[tmp.x][tmp.y] != 'X')
{
if(bj[tmp.x][tmp.y] == 0)
{
bj[tmp.x][tmp.y] = 1;
s[t++] = tmp;
tf = 1;
break;
}
}
}
}
if(!tf)
{
t--;
if(t == 0)
break;
s[t - 1].n++;
bj[s[t].x][s[t].y] = 0;
}
}
if(flag)
cout << "NO" <<endl;
}
return 0;
}
看栈结构体,除了常规的x,y,t之外,还有个n变量,他就是用来保存他的下一步遍历方向,然后在回退的时候注意不再走之前走过的路。因为回退的时候会清标记,所以如果能走之前走过的路,将会进入死循环。
也就是这个原因,在回退的时候不仅需要注意吐栈顶,还有注意更改之前元素的方向,已经清楚退出元素的标记,所以在继续遍历的时候一定要避开。
2015-02-12
最后,啸爷终于给我了他写的手写递归栈,居然过了。。。。研究一个下午也不明白他是怎么过的,算了以后就这么写吧。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#pragma comment(linker, "/STACK:1024000000")
#define EPS (1e-8)
#define LL long long
#define ULL unsigned long long
#define _LL __int64
#define INF 0x3f3f3f3f
#define Mod 100007
using namespace std;
int jx[] = {-1, 0, 1, 0};
int jy[] = { 0,-1, 0, 1};
bool vis[10][10];
char Map[10][10];
struct N
{
int x,y,c,dir;
}st[55*10*10],f,t;
bool Judge(int x,int y,int n,int m)
{
return (1 <= x && x <= n && 1 <= y && y <= m && Map[x][y] != 'X');
}
int main()
{
int i,j,n,m,k;
while(scanf("%d %d %d",&n,&m,&k) && (n||m||k))
{
for(i = 1;i <= n; ++i)
scanf("%s",Map[i]+1);
int sx = -1,sy = -1,ex = -1,ey = -1;
for(i = 1;i <= n; ++i)
{
for(j = 1;j <= m; ++j)
if(Map[i][j] == 'S')
sx = i,sy = j;
else if(Map[i][j] == 'D')
ex = i,ey = j;
}
if(sx == -1 || ex == -1 || (abs(ex-sx) + abs(ey-sy))%2 != k%2 )
{
puts("NO");
continue;
}
memset(vis,false,sizeof(vis));
vis[sx][sy] = true;
st[0] = (N){sx,sy,0,-1};
int Top = 0,site;
while(Top > -1)
{
f = st[Top];
site = Top;
if(Map[f.x][f.y] == 'D' && f.c == k)
break;
if(f.dir == 3 || f.c > k)
{
Top--;
vis[f.x][f.y] = false;
continue;
}
st[site].dir = ++f.dir;
t.x = jx[f.dir] + f.x;
t.y = jy[f.dir] + f.y;
t.c = f.c + 1;
t.dir = -1;
if(Judge(t.x,t.y,n,m) == false || vis[t.x][t.y])
continue;
vis[t.x][t.y] = true;
st[++Top] = t;
}
if(Top > -1)
puts("YES");
else
puts("NO");
}
return 0;
}
汉密尔顿图
基本概念
汉密尔顿通路:给定图G,若存在一条经过图中的每个顶点一次且仅一次的通路,则称这条通路为汉密尔顿通路。
哈密尔顿回路:若存在一条回路,经过图中的每个顶点一次且仅一次,则称这条回路为汉密尔顿回路。
汉密尔顿图:具有汉密尔顿回路的图称为汉密尔顿图。
相关定理
定理1:若无相连通图G(V,E)具有汉密尔顿回路,则对于顶点集合V的人已非空子集S,均有W(G-S)<=|S|成立。其中|S|表示集合S中边的数目,W(G-S)表示G-S中连通分量的数目。
但是注意,用定理1来证明某一个特定图是非汉密尔顿图,这个方法并不是总是有效的,比如彼得森图符合定理1但是属于非汉密尔顿图。
定理2:设G是具有n个顶点的简单图,如果G中每一对顶点度数之和大于等于n-1,则在G中存在一条汉密尔顿回路。
定理3:设G是具有n个顶点的简单图,如果G中每一对顶点度数之和大于等于n,则在G中存在一条汉密尔顿回路。
注意:定理2和定理3是充分关系。
Copyright © 2020 Powered by MWeb, Theme used GitHub CSS.