今天进行到DFS&&BFS&&活动网络问题。BFS和DFS可以解决很多有趣的问题，而BFS和DFS本身就有很多优化、变形。对于对于优化最常见的莫过于剪枝了，而对于搜索剪枝，最常见的也就是奇偶剪枝。

对于DFS，详情见数据结构之图的遍历。

对于DFS剪枝，那ZOJ2110作为例子：Tempter of the Bone。

先看没有剪枝和剪枝之后的效果：

为什么剪枝

因为DFS和BFS可以是认为树形搜索的。因此，他们的搜索轨迹可以生成出深度优先生成树和广度优先生成树，详情见: 图的连通性。

如果我们在生成树的过程中（就是查找过程中），发现并确定一个分支不可能找到解，那么我们就把这个分支剪掉，以节省时间。这就是剪枝。

奇偶剪枝

首先我们要知道一个前提：

奇数 + 偶数 = 奇数
偶数 + 偶数 = 偶数

那么，也就可以推出：

偶数 = 奇数 - 奇数

偶数 = 偶数 - 偶数

假设有这么一个地图：

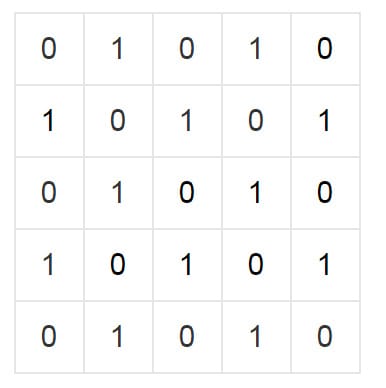
我们可以发现一个规律，从其中任意一个0到任意一个0需要偶数步，而其中任意一个1到任意一个0需要奇数步。

如果我们每一步的消耗时间是相同的，那么，需要用时和最短的步数必须需要同奇偶才能到达，否者不会到达。

为了方便描述，我们假设我们在（sx，sy）的位置，需要消耗t时到达（ex，ey）。

那么不管我们怎么绕圈，如果 t-[abs(ex-sx)+abs(ey-sy)] 结果为非偶数（奇数），则无法在t步恰好到达。

因此，这样我们就可以在搜索过程中，实时判断现在剩下的时间和现在位置到目的地最短距离是否同奇偶，如果不是，那么就没有必要搜索下去了。

骨头问题

再回到ZOJ2110，这个题用到了奇偶剪枝，并且还有一种搜索前优化，就是如果所有狗狗能走的位置（所有的地图位置的个数减去障碍物的个数）小于规定时间，直接打印NO（就是狗狗根本跑不开，就不用搜索了）。

代码：

#include <iostream>
#include <cstring>
#include <cmath>

using namespace std;

char mp[10][10];
int bj[10][10];
int chx[] = {0,1,0,-1};
int chy[] = {1,0,-1,0};
int n,m,t;
int ex,ey;
int tf;

void dfs(int x,int y,int tim)
{
    if(x < 0 || y < 0 || x >= n || y >= m)
        return ;

    if(tim == t && x == ex && y == ey)
    {
        cout << "YES" << endl;
        tf = 1;
        return ;
    }

    int tmp = (t - tim) - fabs(x - ex) - fabs(y - ey);

    if(tmp < 0 || tmp % 2)
        return ;

    for(int i = 0; i < 4;i++)
    {
        if(mp[x + chx[i]][y + chy[i]] != 'X')
        {
            mp[x + chx[i]][y + chy[i]] = 'X';
            dfs(x + chx[i],y + chy[i],tim + 1);
            if(tf)
                return ;
            mp[x + chx[i]][y + chy[i]] = '.';
        }
    }
}

int main()
{
    while(cin >> n >> m >> t,n)
    {
        tf = 0;
        memset(bj,-1,sizeof(bj));
        for(int i = 0;i < n;i++)
            cin >> mp[i];

        int x,y;

        for(int i = 0;i < n;i++)
        {
            int j;
            for(j = 0;j < m;j++)
                if(mp[i][j] == 'S')
                {
                    x = i;
                    y = j;
                    break;
                }
            if(j < m)
                break;
        }

        for(int i = 0;i < n;i++)
        {
            int j;
            for(j = 0;j < m;j++)
                if(mp[i][j] == 'D')
                {
                    ex = i;
                    ey = j;
                    break;
                }
            if(j < m)
                break;
        }

        mp[x][y] = 'X';
        dfs(x,y,0);

        if(!tf)
            cout << "NO" << endl;
    }
    return 0;
}