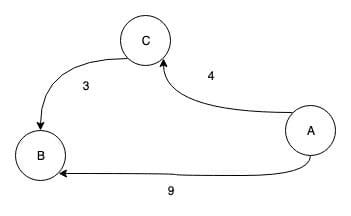
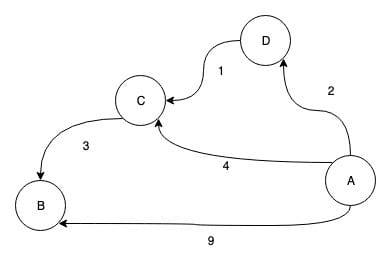
再说并查集
上一次写并查集是在看《数据结构》的时候写了树模型的拓展,当时那一章讲到了并查集,并提出了基本的思想。
并查集是我在第一次寒假集训学到的,当时学完写了总结月球美容计划之并查集。
今天在看生成树的时候,图论那本书又讲到了并查集。
经过各种资料的查阅,确定并查集并没有特别深入的应用,并查集只不过就是一种判断集合属性的方法,说白了,就是有若干种关系,判断谁和谁是同一种关系。
并查集算法是由3个函数组成的,就三个函数:
初始化函数
根据初始化的不同,并查集有两种写法,这两种写法没有优劣差异,就是初始化不同而已。
初始化为-1
int bc[100];
int UFset1()
{
for(int i = 0;i < 100;i++)
bc[i] = -1;
}
初始化为-1是《数据结构》和《图论》都采取的方法,但我学的时候是使用的第二种初始化
初始化为下标
int UFset2()
{
for(int i = 0;i < 100;i++)
bc[i] = i;
}
初始化的不同,在剩下两个函数直接造成细节上的差异,但是并没有造成时间复杂度和空间复杂度的差异。
查找函数
查找函数便是用来查找任一元素的根结点(祖先),而在并查集算法中,唯一的优化便是对查找函数的优化。
未优化的查找函数
//初始化为-1
int fin1 (int a) //查
{
int r = a;
while (-1 != bc[r])
r = bc[r];
return r;
}
//初始化为下标
int fin2 (int a) //查
{
int r = a;
while (r != bc[r])
r = bc[r];
return r;
}
因为并查集数组bc[],存储的是当前结点的父结点,溯流而上,就能找到根结点,找到之后便返回根结点。
对查找函数的优化
//初始化为-1
int fin1 (int a) //查
{
int r = a;
while (-1 != bc[r])
r = bc[r];
while (r != bc[a]) //优化,压缩路径
{
int t = bc[a];
a = bc[a];
bc[t] = r;
}
return r;
}
//初始化为下标
int fin2 (int a) //查
{
int r = a;
while (r != bc[r])
r = bc[r];
while (r != bc[a]) //优化,压缩路径
{
int t = bc[a];
a = bc[a];
bc[t] = r;
}
return r;
}
因为bc数组是记录前驱(父结点)的一棵多叉树,那么如果存在最坏情况(整棵树是线形存在),那么每次查找将最高消耗O(n),也就是说,如果树的深度越低,那么,查找效率越高。因此对其优化、压缩路径。
合并函数
我们可以用查找函数来判断是非属于同一个集合,用合并函数来把两个集合合并成一个集合。
对于合并集合,函数,初始化成什么对其没有影响。
void Union(int R1,int R2)
{
int fa = fin(R1),fb = fin(R2);
bc[fa] = fb;
}
进一步优化
在图论这本书了提到了一个灰常奇妙的优化。
原理很简单,这个并查集浪费时间在查找上,因为如果树长的很奇葩(线形),那么查找时间将灰常壮观,因此,在查找函数中对其压缩路径,来解决这个问题,那么压缩完路径之后,深度不超过3,那么,查找的时间复杂度解决了,但是还有一个东西浪费时间,就是压缩路径本身。
这样想,如果我们在建树的过程中就尽量让树平衡(相关概念参考:数据结构之二叉树),那么在压缩路径的时候,也会节省一些时间。
至于怎么实现,书中给出的解决方案是靠根结点来记录这个根结点下有多少子节点。
首现,要选择初始化为-1的那种方案,然后对查找进行修改
//初始化为-1
int fin1 (int a) //查
{
int r = a;
while (bc[r] >= 0) //在这里修改了,
r = bc[r]; //因为如果是根结点,其值为负数而不仅为-1
while (r != bc[a]) //优化,压缩路径
{
int t = bc[a];
a = bc[a];
bc[t] = r;
}
return r;
}
然后对合并函数进行修改:
void Union(int R1,int R2)
{
int fa = fin(R1),fb = fin(R2);
int tmp = bc[fa] + bc[fb]; //结点个数、负数
if(bc[fa] > bc[fb]) //加权法则
{
bc[fa] = fb;
bc[fb] = tmp;
}else
{
bc[fb] = fa;
bc[fa] = tmp;
}
}
深度优先搜索(DFS)的奇偶剪枝
今天进行到DFS&&BFS&&活动网络问题。BFS和DFS可以解决很多有趣的问题,而BFS和DFS本身就有很多优化、变形。对于对于优化最常见的莫过于剪枝了,而对于搜索剪枝,最常见的也就是奇偶剪枝。
对于DFS,详情见数据结构之图的遍历。
对于DFS剪枝,那ZOJ2110作为例子:Tempter of the Bone。
先看没有剪枝和剪枝之后的效果:

为什么剪枝
因为DFS和BFS可以是认为树形搜索的。因此,他们的搜索轨迹可以生成出深度优先生成树和广度优先生成树,详情见: 图的连通性。
如果我们在生成树的过程中(就是查找过程中),发现并确定一个分支不可能找到解,那么我们就把这个分支剪掉,以节省时间。这就是剪枝。
奇偶剪枝
首先我们要知道一个前提:
奇数 + 偶数 = 奇数
偶数 + 偶数 = 偶数
那么,也就可以推出:
偶数 = 奇数 - 奇数
偶数 = 偶数 - 偶数
假设有这么一个地图:
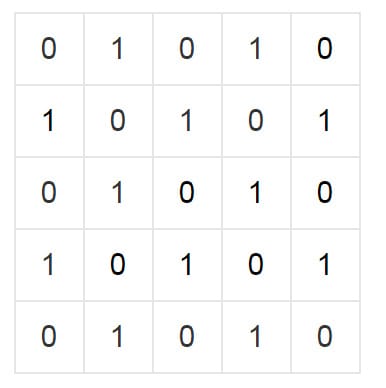
我们可以发现一个规律,从其中任意一个0到任意一个0需要偶数步,而其中任意一个1到任意一个0需要奇数步。
如果我们每一步的消耗时间是相同的,那么,需要用时和最短的步数必须需要同奇偶才能到达,否者不会到达。
为了方便描述,我们假设我们在(sx,sy)的位置,需要消耗t时到达(ex,ey)。
那么不管我们怎么绕圈,如果 t-[abs(ex-sx)+abs(ey-sy)] 结果为非偶数(奇数),则无法在t步恰好到达。
因此,这样我们就可以在搜索过程中,实时判断现在剩下的时间和现在位置到目的地最短距离是否同奇偶,如果不是,那么就没有必要搜索下去了。
骨头问题
再回到ZOJ2110,这个题用到了奇偶剪枝,并且还有一种搜索前优化,就是如果所有狗狗能走的位置(所有的地图位置的个数减去障碍物的个数)小于规定时间,直接打印NO(就是狗狗根本跑不开,就不用搜索了)。
代码:
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
char mp[10][10];
int bj[10][10];
int chx[] = {0,1,0,-1};
int chy[] = {1,0,-1,0};
int n,m,t;
int ex,ey;
int tf;
void dfs(int x,int y,int tim)
{
if(x < 0 || y < 0 || x >= n || y >= m)
return ;
if(tim == t && x == ex && y == ey)
{
cout << "YES" << endl;
tf = 1;
return ;
}
int tmp = (t - tim) - fabs(x - ex) - fabs(y - ey);
if(tmp < 0 || tmp % 2)
return ;
for(int i = 0; i < 4;i++)
{
if(mp[x + chx[i]][y + chy[i]] != 'X')
{
mp[x + chx[i]][y + chy[i]] = 'X';
dfs(x + chx[i],y + chy[i],tim + 1);
if(tf)
return ;
mp[x + chx[i]][y + chy[i]] = '.';
}
}
}
int main()
{
while(cin >> n >> m >> t,n)
{
tf = 0;
memset(bj,-1,sizeof(bj));
for(int i = 0;i < n;i++)
cin >> mp[i];
int x,y;
for(int i = 0;i < n;i++)
{
int j;
for(j = 0;j < m;j++)
if(mp[i][j] == 'S')
{
x = i;
y = j;
break;
}
if(j < m)
break;
}
for(int i = 0;i < n;i++)
{
int j;
for(j = 0;j < m;j++)
if(mp[i][j] == 'D')
{
ex = i;
ey = j;
break;
}
if(j < m)
break;
}
mp[x][y] = 'X';
dfs(x,y,0);
if(!tf)
cout << "NO" << endl;
}
return 0;
}
可图和Havel-Hakimi定理
可图(Graphic)
什么是可图,那需要先说一下度序列。
度序列是把图的多有顶点度数排列成一个序列s,则称s为图G的度序列。
度序列可以是按照顶点的顺序排列,也可以按照递增、递减的顺序排列。所谓的可图,是建立在度序列的基础上的。
序列是可图的:一个非负整数组成的有限序列如果是某个无向图的度序列,则称这个序列是可图的。
说白了,就是如果一串度序列可以逆向生成出图,就是可图的。而判断一个序列是否是可图的,则由Havel-Hakimi定理判断。
Havel-Hakimi定理
由非负整数组成的非增序列s:d1,d2,...,dn(n>=2,d1>=1)是可图的,当且仅当序列:
s1:d2 - 1,d3 - 1,...,dd1+1 - 1,dd1+2,...,dn
是可图的。序列s1中有n-1个非负整数,s序列中d1后的前d1个度数(即d2~dd1+1)减1后构成s1中的前d1个数。
说白了就是先把第一个点(度数为d1)连线到后面d1个点,保证第一个点度数满足,然后再以此类推考虑后面的点。如果后面所有顶点满足并且度数不多不少(最后不剩,过程中没有度数为负数),即可认为,度序列是可图的。
青蛙邻居问题
POJ1659 Frogs' Neighborhood
Description
未名湖附近共有N个大小湖泊L1, L2, ..., Ln(其中包括未名湖),每个湖泊Li里住着一只青蛙Fi(1 ≤ i ≤ N)。如果湖泊Li和Lj之间有水路相连,则青蛙Fi和Fj互称为邻居。现在已知每只青蛙的邻居数目x1, x2, ...,xn,请你给出每两个湖泊之间的相连关系。
Input
第一行是测试数据的组数T(0 ≤ T ≤ 20)。每组数据包括两行,第一行是整数N(2 1, x2,..., xn(0 ≤ xi ≤ N)。
Output
对输入的每组测试数据,如果不存在可能的相连关系,输出"NO"。否则输出"YES",并用N×N的矩阵表示湖泊间的相邻关系,即如果湖泊i与湖泊j之间有水路相连,则第i行的第j个数字为1,否则为0。每两个数字之间输出一个空格。如果存在多种可能,只需给出一种符合条件的情形。相邻两组测试数据之间输出一个空行。
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int G[20][20];
struct Node
{
int dnum;
int no;
}d[20];
int cmp(Node a,Node b)
{
return a.dnum > b.dnum;
}
int main()
{
int N;
cin >> N;
while(N--)
{
bool flag = 1;
memset(G,0,sizeof(G));
int n;
cin >> n;
for(int i = 0;i < n;i++)
{
cin >> d[i].dnum;
d[i].no = i;
}
for(int i = 0;i < n;i++)
{
sort(&d[i],&d[i] + n - i,cmp);
int last = d[i].dnum;
d[i].dnum = 0;
if(last > n - i)
{
flag = 0;
break;
}
for(int j = i + 1;j <= i + last;j++)
{
if(d[j].dnum - 1 >= 0)
{
G[d[i].no][d[j].no] = 1;
G[d[j].no][d[i].no] = 1;
d[j].dnum -= 1;
}else
{
flag = 0;
}
if(!flag)
break;
}
if(!flag)
break;
}
if(flag)
{
for(int i = 0;i < n;i++)
if(d[i].dnum > 0)
flag = 0;
}
if(!flag)
cout << "NO" << endl;
else
{
cout << "YES" << endl;
for(int i = 0;i < n;i++)
for(int j = 0;j < n;j++)
cout << G[i][j] << (j < n - 1 ? ' ' : 'n');
}
if(N)
cout << endl;
}
return 0;
}
注意
这个题目是Special Judge,也就是说这个题的答案是有多种的。这个是由Havel-Hakimi定理导致的,由于可图是由度数重构图,这个过程构建的图可能不是唯一的。
Copyright © 2020 Powered by MWeb, Theme used GitHub CSS.