弗洛伊德算法，是当时集训的时候学最短路问题的第一个算法（去年寒假），当时学长直说这个算法好写、时间复杂度高，至于这个算法是什么原理却没有讲。学长说，照着敲就可以，循环敲对了，就那么神奇的对了，循环顺序错了，就神奇的 WA 了。

今年寒假，我也是学长了，逗比硕把最短路这一课给我了，这一周我要给学弟学妹们讲搜索和最短路。

搜索有 BFS 和 DFS 两个算法，或者说是搜索思想，而最短路有 4 个算法。最近也重点看了搜索和最短路，翻来覆去好几遍。然后对搜索和走最短路的各个算法都有了进一步的理解，终于对这几种东西不再是仅限于会用模板了。

在与学弟的交流并解决学弟的疑问的同时，也让我看到的搜索和最短路那些只抄模板很容易忽略的地方。以及之前自己没有注意到的东西。

之前最短路的总结就写过弗洛伊德。但没有解释弗洛伊德，这篇文章主要解释弗洛伊德原理。

首先要明确，弗洛伊德是求任意两点之间的最短路。此处记录任意两点之间的距离是靠一个二维数组（示例里的 G数组）实现的。

摆出弗洛伊德的示例代码：

int fld (int n,int s,int e)
{
    int d[200][200];
    int i,j,k;
    // G 是一个存储了整张图的邻接矩阵
    memcpy(d,G,sizeof(G));

    for (k = 1;k <= n;k++)
        for (i = 1;i <= n;i++)
            for (j = 1;j <= n;j++)
                d[i][j] = qmin (d[i][j],d[i][k] + d[k][j]);

    return d[s][e];
}

然后说弗洛伊德是怎么实现的。

初始化时，有个 d数组（见上方代码），是 G 数据的一个复制，我们可以认为，这个 d 开始的时候是和 G 的含义一致即任意两个点之间相连的距离。换句话说，就是如果两个点 p1 和 p2 有相连的边，d[p1][p2] 就是一个描述两点距离的值，否则就是正无穷（这里用 int 最大值表示）。

然后进入循环，从k = 1开始，也就是从 1号点 开始，对于任意两个点做一个尝试：能不能把1号点放入他们中间。

如果说一开始 d数组 表示的是任意两点直连路径，那经过第一次循环之后，d数组 所代表的含义已经变了，现在的 d数组 可以理解为任意两点之间中间点不超过1个点的最短路径。

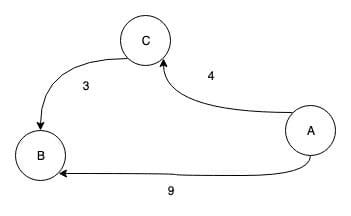
为什么是不超过一个点的最短路径呢？因为刚才把 1号点 尝试放入任意两个点中间，如果发现放入就会更新最短路，那么便会更新 d数组。换句话说，如果 A 到 B 的距离大于 A 到 C 然后到 B 的距离，那么这个 C 点就可以放入最短路。与此相同，如果有的可以放入 1号点，有的放入对最短路没有改善，那么 d 数组就是存储的任意两个点之间不超过1个点的最短路。

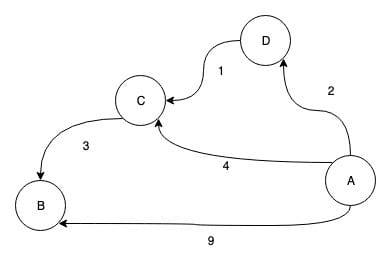
然后循环继续 k=2，那么，又开始在任意两个点之间尝试把 2号点 放入最短路中，依然是部分可以优化最短路，部分不可以。而且经过第一次循环之后，d数组 是任意两点中间点不超过 1 个点的最短路。而尝试把 2号点 放入则会让 d数组 变成任意两个点的中间点不超过 2 个点的最短路。

以此类推，把所有点循环完后，就认为 d数组 是存储的任意两个点之间中间点不超过 n 个点的最短路，实际上，这时候的 d 已经是站在全局上考虑的解了，而且对于一个 n 个点的图来说，他的最短路的中间点一定小于 n，那么我们就认为，这时候的任意两个点的最短路实际上就是 d数组 所描述的解。

算法的魅力不在于用这个算法A掉了一个或更多的题目，而是这个算法本身！