什么是双向BFS
双向BFS在寒假解决图论中搜索问题时就已经遇到了,单向BFS是从一个起点到一个终点搜索,找最短路,而双向BFS是不仅从起点到终点搜索,而且同时从终点出发,向起点进行搜索。双向BFS看起来能快很多。
当时和龙哥讨论,感觉双向BFS理论上不会快到哪去,毕竟搜索就是枚举的过程,加上当时我还不会双向BFS,就没有细究。
双向BFS为什么快
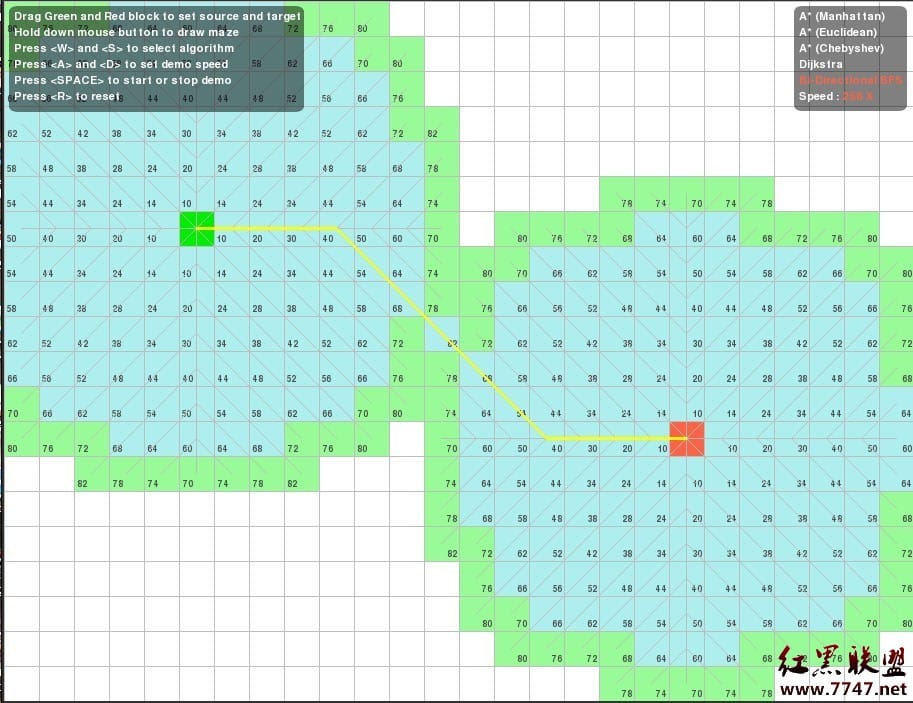
昨天开始学双向BFS并拿了一个题进行试验,发现双向BFS的确快(有图有真相):

第一次提交(11:46)是用普通的BFS写的,然后在普通的BFS基础上改为了双向BFS然后提交发现确实快了。
双向BFS为什么快本身就是个很奇妙的问题,有两张图也许能很好的说明问题:

单向BFS(上图)
双向BFS(上图)
(图出自:红黑联盟)
如果把搜索看成一个圆,那么圆的面积可以看做能表示搜索次数的一个值。而起点s和终点e之间的距离可以大体看为园的半径。
对于单向BFS(第一个图)来说,假设路径为L,那么搜索次数为 LLPI(PI为圆周率)。
对于双向BFS(第二个图)来说,假设路径为L,那么搜索次数为2*(L/2)*(L/2)*PI。
相比较来说,的确可以节省很多时间,而能节省多少是根据图的大小和L的大小来决定的,图越大,L越小,节省时间越明显。
双向BFS怎么实现
双向BFS有好几种实现,我只说我自己用的这种。
先贴出HDU1195题的单向BFS和双向BFS代码,不同之处显而易见:
单向:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct Node
{
int num;
int t;
};
int bj[10000];
void fen(int num[4],int n)
{
num[0] = n / 1000;
num[1] = (n / 100) % 10;
num[2] = (n / 10) % 10;
num[3] = n % 10;
}
int he(int num[4])
{
int sum = 0;
for(int i = 0;i < 4;i++)
sum = sum * 10 + num[i];
return sum;
}
int bfs(int s,int e)
{
queue<Node> que;
while(!que.empty())
que.pop();
Node now,tmp;
now.num = s;
now.t = 0;
que.push(now);
bj[now.num] = 1;
while(!que.empty())
{
now = que.front();
que.pop();
if(now.num == e)
return now.t;
int tn[4];
//枚举每一位
for(int i = 0;i < 4;i++)
{
//加一
fen(tn,now.num);
tn[i] += 1;
if(tn[i] == 10)
tn[i] = 1;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = 1;
que.push(tmp);
}
//减一
fen(tn,now.num);
tn[i] -= 1;
if(tn[i] == 0)
tn[i] = 9;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = 1;
que.push(tmp);
}
}
//交换相邻两个数位置
for(int i = 0;i < 3;i++)
{
fen(tn,now.num);
tn[i] ^= tn[i + 1];
tn[i + 1] ^= tn[i];
tn[i] ^= tn[i + 1];
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = 1;
que.push(tmp);
}
}
}
return -1;
}
int main()
{
int N;
cin >> N;
while(N--)
{
int num1,num2;
memset(bj,0,sizeof(bj));
cin >> num1 >> num2;
int ans = bfs(num1,num2);
cout << ans << endl;
}
}
双向:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct Node
{
int num;
int t;
};
int bj[10000];
int ti[10000];
void fen(int num[4],int n)
{
num[0] = n / 1000;
num[1] = (n / 100) % 10;
num[2] = (n / 10) % 10;
num[3] = n % 10;
}
int he(int num[4])
{
int sum = 0;
for(int i = 0;i < 4;i++)
sum = sum * 10 + num[i];
return sum;
}
int bfs(int s,int e)
{
queue<Node> que;
while(!que.empty())
que.pop();
Node now,tmp;
now.num = s;
now.t = 0;
que.push(now);
bj[now.num] = 1;
now.num = e;
now.t = 0;
que.push(now);
bj[now.num] = 2;
while(!que.empty())
{
now = que.front();
que.pop();
int tn[4];
//枚举每一位
for(int i = 0;i < 4;i++)
{
//加一
fen(tn,now.num);
tn[i] += 1;
if(tn[i] == 10)
tn[i] = 1;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = bj[now.num];
ti[tmp.num] = tmp.t;
que.push(tmp);
}else if(bj[tmp.num] != bj[now.num])
{
return ti[tmp.num] + ti[now.num] + 1;
}
//减一
fen(tn,now.num);
tn[i] -= 1;
if(tn[i] == 0)
tn[i] = 9;
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = bj[now.num];
ti[tmp.num] = tmp.t;
que.push(tmp);
}else if(bj[tmp.num] != bj[now.num])
{
return ti[tmp.num] + ti[now.num] + 1;
}
}
//交换相邻两个数位置
for(int i = 0;i < 3;i++)
{
fen(tn,now.num);
tn[i] ^= tn[i + 1];
tn[i + 1] ^= tn[i];
tn[i] ^= tn[i + 1];
tmp.num = he(tn);
tmp.t = now.t + 1;
if(bj[tmp.num] == 0)
{
bj[tmp.num] = bj[now.num];
ti[tmp.num] = tmp.t;
que.push(tmp);
}else if(bj[tmp.num] != bj[now.num])
{
return ti[tmp.num] + ti[now.num] + 1;
}
}
}
return -1;
}
int main()
{
int N;
cin >> N;
while(N--)
{
int num1,num2;
memset(bj,0,sizeof(bj));
cin >> num1 >> num2;
int ans = bfs(num1,num2);
cout << ans << endl;
}
}
两份代码一共有两大区别,一个是标记数组,一个是记录到当前位置的距离数组。
第一个大区别就是标记,单向BFS的标记很单纯,就是标记有没有走过,而双向BFS不仅标记有没有走过,还进行区分标记,来记录到底是从起点走到当前点的还是从终点走到当前点的。也可以认为这是不同的两层搜索同时进行,分别标记。如果两层标记相遇,就认为已经找到了一条路径连通了起点和终点。
第二大区别就是距离数组,单向BFS不需要这个数组因为队列里的t变量就足够记录到当前位置的最短路(如果当前位置为终点,这个最短路就是答案)。而双向这个t的含义是从起点到当前位置的最短距离,因为有两个起点,所以不能记录两条路径(不同起点)的路径和,因此需要一个距离数组保存不同路径到当前位置的距离,当两条路径相接之后,只需要将保存接触点的距离相加便是答案。


