今天被这个叫Fleury算法的东西折磨了一下午，这个算法是解决欧拉回路问题的，其实已经被欧拉回路折磨两天了。

图论这本书本是打算一个寒假解决掉的，最初的时候认为会卡到第六章网络流部分，没想到在第五章可行性遍历就卡了。

首先是欧拉图，然后就是DFS解决欧拉图顺序问题，今天又卡到了佛罗莱算法，简直了。

佛罗莱算法是用来求欧拉回路的，判断欧拉回路十分简单，但是求欧拉回路一般是用DFS解决，但是DFS时间复杂度有些高，而佛罗莱算法能把时间复杂度压缩到O(e * e)，e是边的数量。

原理：

任取v0∈V(G)，令P0=v0；

设Pi=v0e1v1e2…ei vi已经行遍，按下面方法从中选取ei+1：

（a）ei+1与vi相关联；

（b）除非无别的边可供行遍，否则ei+1不应该为Gi=G-{e1,e2, …, ei}中的桥（所谓桥是一条删除后使连通图不再连通的边）；

（c）当（b）不能再进行时，算法停止。

可以证明,当算法停止时所得的简单回路Wm=v0e1v1e2….emvm(vm=v0)为G中的一条欧拉回路。

当然，这个“可以证明”我还暂时证明不出来= =。

佛罗莱算法还是使用了DFS，其中这DFS的目的在于找出“桥”，当删掉一些边后整个图不连通，而最后删掉恰好不连通的那个边正是桥。

然后遇到桥之后栈回退不走桥（保证为走过的图还是连通）然后选择其他非桥的路进行继续入栈保存并继续DFS删边找桥。

有一点需要注意，就是栈里存储了什么，开始的时候我以为是路线，所以对这个算法一直想不明白，就在刚才我突然想到，我们找的是欧拉回路，也就是说起点就是终点，而对于桥的两个点都是两个回路，我们大可放心把桥的一段压在栈里不打印而继续都是把桥的另一端搜索完再打印，效果是一样的。

比如图：

如果以2开始，进行2 3 4 5 3 2 8 2的顺序进行遍历，在8到2的时候进入了死胡同，正是因为在8的时候进入桥（e9让2和其他结点断开）

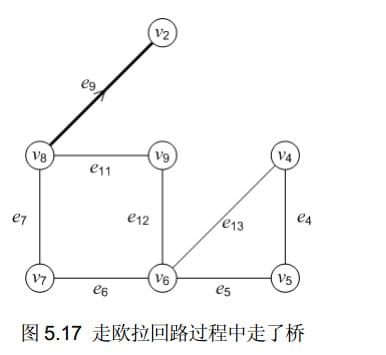
如果在8的时候转向，开始9或7的继续遍历边解决这个问题，但是我的疑惑便是，因为刚开始的遍历到8为止，所有路线都存储在栈里，而退出的过程需要打印8，也就是说打印完8之后就不管之前入栈的结点而继续向下遍历，为什么还能保证正确。

因为8换方向遍历然后入栈的依然是（子图的）欧拉回路，也定将以8结束来上（刚才留下的）桥进行最后的遍历。而所谓的最后遍历也就是刚才已经留在栈中的结点。

因此栈是存储的路径但不是遍历路径而是存储了一个保证正确但不保证和遍历顺序相同的路径（在遇到桥的时候可能会导致最后退栈逆序）。

Fleury实现：

#include <iostream>
#include <math.h>
#include <algorithm>
#include <cstring>
#include <stack>

#define INF 100000

using namespace std;

int G[100][100];
int n;
stack<int> s;

void dfs(int x)
{
    s.push(x);

    for(int i = 1; i <= n; i++)
    {
        if(G[i][x] > 0)
        {
            G[x][i] = 0;
            G[i][x] = 0;
            dfs(i);
            break;
        }
    }
}

void fleury(int x)
{
    int b;
    s.push(x);

    while(!s.empty())
    {
        b = 0;
        for(int i = 1; i <= n; i++)
        {
            if(G[s.top()][i] > 0)
            {
                b = 1;
                break;
            }
        }
        if(b == 0)
        {
            cout << s.top() << " ";
            s.pop();
        }
        else
        {
            int t = s.top();
            s.pop();
            dfs(t);
        }
    }
}

int main()
{
    int m;
    while(cin >> n >> m,n)
    {
        while(!s.empty())
            s.pop();
        memset(G,0,sizeof(G));
        for(int i = 0; i < m; i++)
        {
            int a,b;

            cin >> a >> b;
            G[a][b] = 1;
            G[b][a] = 1;
        }
        int num = 0;
        int start = 2;
        for(int i = 1; i <= n; i++)
        {
            int d = 0;
            for(int j = 1; j <= n; j++)
                d += G[i][j];
            if(d % 2 == 1)
            {
                start = i;
                num++;
            }
        }

        if(num == 0 || num == 2)
            fleury(start);
        else
            cout << "No Euler path" << endl;
    }
    return 0;
}