树的遍历
遍历二叉树
在二叉树的一些应用中,常常要求在树中查找具有某种特征的结点,或者对树中全部结点逐一进行某种处理,这就提出了一个遍历二叉树的问题。即如何按某条搜索路径巡防树中每个结点,使得每个节点均被访问一次,而且仅被访问一次。 因为二叉树是由3个基本单元组成:根结点,左子树和右子树。因此,若能依次遍历这三个部分,便是遍历了整个二叉树。根据对这三个部分遍历顺序不同,那么我们就有了先序遍历,中序遍历,后序遍历。 先序遍历: 若二叉树为空则空操作(递归边界),否者: 1.访问根节点 2.先序遍历左子树 3.先序遍历右子树 中序遍历: 若二叉树为空则空操作,否者: 1.中序遍历左子树 2.访问根节点 3.中序遍历右子树 后序遍历: 若二叉树为空则空操作,否者: 1.后序遍历左子树 2.后序遍历右子树 3.访问根节点 这个过程明显是个递归的过程,《数据结构》给出了先序遍历的伪代码:
Status PreOrderTraverse( BiTree T, Status(*Visit)(ElemType) ) {
// 采用二叉链表存储结构,Visit是对数据元素操作的应用函数,
// 先序遍历二叉树T的递归算法,对每个数据元素调用函数Visit。
// 最简单的Visit函数是:
// Status PrintElement( ElemType e ) { // 输出元素e的值
// printf( e ); // 实用时,加上格式串
// return OK;
// }
// 调用实例:PreOrderTraverse(T, PrintElement);
if (T) {
if (Visit(T->data))
if (PreOrderTraverse(T->lchild, Visit))
if (PreOrderTraverse(T->rchild, Visit)) return OK;
return ERROR;
} else return OK;
} // PreOrderTraverse
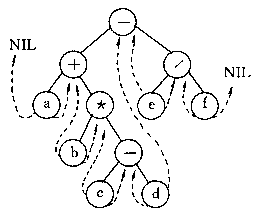
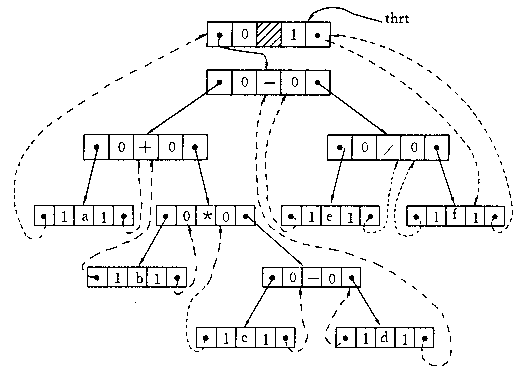
对于上图的树(忽略他的线索线),如果我们采用不同的遍历方式,可以得到不同的结果: 先序遍历:-+ab-cd/ef 中序遍历:a+bc-d-e/f 后序遍历:abcd-*+ef/- 其实这就是前缀表达式(波兰式),中缀表达式,后缀表达式(逆波兰式)。 其实用树便可以实现前缀、中缀、后缀表达式相互转换,但是,一般我们采用栈的方式实现,至少不用建树。 仿照递归算法执行过程中递归工作栈的状态变化状态可直接写出相应的非递归算法。例如,从中序遍历递归算法执行过程中递归工作栈的状态可见: 1.工作记录中包含两项其一是递归调用的语句编号,其二是指向左子树根的指针进栈 2.若栈顶记录中的指针值为空,则应退至上一层,若是从左子树返回,则应访问当前层即栈顶记录中指针所指的根结点 3.若是从右子树返回,则表明当前层的遍历结束,应继续退栈。从另一角度,这意味着遍历右子树时不再需要保存当前层指针,直接修改栈顶记录中的指针就好。 非递归算法执行效率要比递归算法高些,有时候可以考虑。
Status InOrderTraverse(BiTree T, Status (*Visit)(ElemType)) {
// 采用二叉链表存储结构,Visit是对数据元素操作的应用函数。
// 中序遍历二叉树T的非递归算法,对每个数据元素调用函数Visit。
stack S;
BiTree p;
InitStack(S); Push(S, T); // 根指针进栈
while (!StackEmpty(S)) {
while (GetTop(S, p) && p) Push(S, p->lchild); // 向左走到尽头
Pop(S, p); // 空指针退栈
if (!StackEmpty(S)) { // 访问结点,向右一步
Pop(S, p);
if (!Visit(p->data)) return ERROR;
Push(S, p->rchild);
}
}
return OK;
} // InOrderTraverse
Status InOrderTraverse(BiTree T, Status (*Visit)(ElemType)) {
// 采用二叉链表存储结构,Visit是对数据元素操作的应用函数。
// 中序遍历二叉树T的非递归算法,对每个数据元素调用函数Visit。
stack S;
BiTree p;
InitStack(S); p = T;
while (p || !StackEmpty(S)) {
if (p) { Push(S, p); p = p->lchild; } // 非空指针进栈,继续左进
else { // 上层指针退栈,访问其所指结点,再向右进
Pop(S, p);
if (!Visit(p->data)) return ERROR;
p = p->rchild;
}
}
return OK;
} // InOrderTraverse
建立二叉树
遍历是二叉树各种操作的基础,可以在遍历过程中对结点进行各种操作,如:对一颗已知树可求结点的双亲,求结点的孩子结点,判断结点所在的层次等。 反之,也可以在遍历过程中生成结点,建立二叉树的存储结构。
BiTree CreateBiTree(BiTree &T) {
// 按先序次序输入二叉树中结点的值(一个字符),空格字符表示空树,
// 构造二叉链表表示的二叉树T。
char ch;
scanf("%c",&ch);
if (ch=='#') T = NULL;
else {
if (!(T = (BiTNode *)malloc(sizeof(BiTNode)))) return ERROR;
T->data = ch; // 生成根结点
CreateBiTree(T->lchild); // 构造左子树
CreateBiTree(T->rchild); // 构造右子树
}
return T;
} // CreateBiTree
对二叉树的遍历的搜索路径除了已经说的先序中序后序遍历,还可以从上到下(DFS),从左到右(BFS)按层次遍历。 但是遍历二叉树的算法中的基本操作时访问结点,则无论安那一种次序进行遍历,对含n个结点的二叉树,其时间复杂度均为O(n),所需辅助空间为遍历过程中栈的最大容量,即树的深度,最坏情况下为n则空间复杂度也为O(n)。
回溯法与树的遍历
在程序设计中有一类求一组解或求全部解或求最优解的问题,比如八皇后问题,骑士周游问题,不是根据某种确定的计算法则,而是利用试探和回溯的搜索技术求解。 回溯法的实质是一个先序遍历一棵“状态树”的过程,只是这棵树不是遍历前预先建立的,而是隐含在遍历过程中的(边建立便遍历,随之释放)。 八皇后问题以后讨论,在数据结构中有一个很好玩的例题。
求含n个元素的集合的幂集 集合A的幂集是由集合A的所有子集所组合的集合。如:A={1,2,3},则A的幂集, p(A)={{1,2,3},{1,2},{1,3},{2,3},{1},{2},{3},∅}
但是这个答案肿么解出来,树中给出了一个树的思想,因为对每个元素只有舍或者留两种情况,那么,我们可以用二叉树,左支是留,右支是舍:

没有比代码更直观的了:
void GetPowerSet(int i, List A, List &B) {
// 线性表A表示集合A,线性表B表示幂集ρ(A)的一个元素。
// 局部量k为进入函数时表B的当前长度。
// 第一次调用本函数时,B为空表,i=1。
ElemType x;
int k;
if (i > ListLength(A)) Output(B); // 输出当前B值,即ρ(A)的一个元素
else {
GetElem(A, i, x); k = ListLength(B);
ListInsert(B, k+1, x); GetPowerSet(i+1, A, B);
ListDelete(B, k+1, x); GetPowerSet(i+1, A, B);
}
} // GetPowerSet
其实还有优化,比如加上状态压缩什么的。当然,这只是在竞赛中的小伎俩罢了。
Copyright © 2020 Powered by MWeb, Theme used GitHub CSS.