这一篇文章继续讲,二叉树是树的特殊,想要熟悉树的模型,就要从二叉树开始,而存储二叉树的二叉链表和三叉链表也是存储任意树的一般方式。
定义
二叉树是一种树型结构,它的特点是每个结点至多只有两颗子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒。
而树的抽象数据类型:
ADT BinaryTree{
//数据对象D:D是具有相同特性的数据元素的集合。
//数据关系R:
// 若D=Φ,则R=Φ,称BinaryTree为空二叉树;
// 若D≠Φ,则R={H},H是如下二元关系;
// (1)在D中存在惟一的称为根的数据元素root,它在关系H下无前驱;
// (2)若D-{root}≠Φ,则存在D-{root}={D1,Dr},且D1∩Dr =Φ;
// (3)若D1≠Φ,则D1中存在惟一的元素x1,<root,x1>∈H,且存在D1
// 上的关系H1 ⊆H;若Dr≠Φ,则Dr中存在惟一的元素xr,<root,xr>∈H,且存在上的关系Hr ⊆H;H={<root,x1>,<root,xr>,H1,Hr};
// (4)(D1,{H1})是一棵符合本定义的二叉树,称为根的左子树;(Dr,{Hr})是一棵符合本定义的二叉树,称为根的右子树。
基本操作:
InitBiTree( &T )
//操作结果:构造空二叉树T。
DestroyBiTree( &T )
// 初始条件:二叉树T已存在。
// 操作结果:销毁二叉树T。
CreateBiTree( &T, definition )
// 初始条件:definition给出二叉树T的定义。
// 操作结果:按definiton构造二叉树T。
ClearBiTree( &T )
// 初始条件:二叉树T存在。
// 操作结果:将二叉树T清为空树。
BiTreeEmpty( T )
// 初始条件:二叉树T存在。
// 操作结果:若T为空二叉树,则返回TRUE,否则返回FALSE。
BiTreeDepth( T )
// 初始条件:二叉树T存在。
// 操作结果:返回T的深度。
Root( T )
// 初始条件:二叉树T存在。
// 操作结果:返回T的根。
Value( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的值。
Assign( T, &e, value )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:结点e赋值为value。
Parent( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:若e是T的非根结点,则返回它的双亲,否则返回“空”。
LeftChild( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的左孩子。若e无左孩子,则返回“空”。
RightChild( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的右孩子。若e无右孩子,则返回“空”。
LeftSibling( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回“空”。
RightSibling( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回“空”。
InsertChild( T, p, LR, c )
// 初始条件:二叉树T存在,p指向T中某个结点,LR为0或1,非空二叉树c与T不相交且右子树为空。
// 操作结果:根据LR为0或1,插入c为T中p所指结点的左或右子树。p所指结点的原有左或右子树则成为c的右子树。
DeleteChild( T, p, LR )
// 初始条件:二叉树T存在,p指向T中某个结点,LR为0或1。
// 操作结果:根据LR为0或1,删除T中p所指结点的左或右子树。
PreOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:先序遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
InOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:中序遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
PostOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:后序遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
LevelOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:层次遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
}ADT BinaryTree
}
基本操作的实现:
//二叉树的结点结构体:
typedef struct{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//二叉树的创建:
/*******************************************/
/* 按照前序遍历建立二叉树 */
/*******************************************/
Status CreateBiTree(BiTree &T)
{
//按先序次序输入二叉树中结点的值(一个字符),
//空格字符表示空树,构造二叉链表表示的二叉树T。
char ch;
ch = getchar();//scanf("%c",&ch);
if(ch == ' ')
T = NULL;
else
{
if(!(T = (BiTNode*)malloc(sizeof(BiTNode))))
exit(OVERFLOW);
T->data = ch; //生成根结点
CreateBiTree(T->lchild); //构造左子树
CreateBiTree(T->rchild); //构造右子树
}
return OK;
}
/************************************************************/
/* 按层次顺序建立一棵二叉树 :队列 */
/************************************************************/
Status LevelCreateBiTree(BiTree &T)
{
BiTree p,s;//p指向父亲结点,s指向孩子结点
Queue BiNodeQueue;
char ch;
ch=getchar();
if(ch==' ')
{
return NULL;
}
T=(BiTNode*)malloc(sizeof(BiTNode)); //生成根结点
T->data=ch;
EnQueue(BiNodeQueue,T); //用队列实现层次遍历
while(!BiNodeQueue.Empty())
{
DeQueue(BiNodeQueue,p);
ch=getchar(); //为了简化操作,分别对左右子结点进行赋值。
if(ch!=' ')//子树不空则进队列进行扩充。下同
{
s=(BiTNode*)malloc(sizeof(BiTNode));
s->data=ch;
p->lchild=s;
EnQueue(BiNodeQueue,s);
}
else
{
p->lchild=NULL;
}
ch=getchar();
if(ch!=' ')
{
s=(BiTNode*)malloc(sizeof(BiTNode));
s->data=ch;
p->rchild=s;
EnQueue(BiNodeQueue,s);
}
else
{
p->rchild=NULL;
}
}
return OK;
}
//2.二叉树的前序遍历:
/*******************************************/
/* 按照前序递归遍历二叉树 */
/*******************************************/
Status PreOrderTraverse(BiTree T)
{
if(T)
{
printf("%d",T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
return OK;
}
/*******************************************/
/* 按照前序非递归遍历二叉树:栈 */
/*******************************************/
Status PreOrderTraverse(BiTree T)
{
stack S;
InitStack(S);
BiTree p=T; //p指向当前访问的结点
while(p||!StackEmpty(S))
{
if(p)
{
printf("%c",p->data);
Push(S,p);
p=p->lchild;
}
else
{
Pop(S,p);
p=p->rchild;
}
}
return OK;
}
//3.二叉树的中序遍历:
/*******************************************/
/* 按照中序递归遍历二叉树 */
/*******************************************/
Status InOrderTraverse(BiTree T)
{
if(T)
{
InOrderTraverse(T->lchild);
printf("%d",T->data);
InOrderTraverse(T->rchild);
}
return OK;
}
/*******************************************/
/* 按照中序非递归遍历二叉树 */
/*******************************************/
Status InOrderTraverse(BiTree T)
{
stack S;
BiTree p;
InitStack(S); Push(S, T);
while (!StackEmpty(S))
{
while (GetTop(S, p) && p)
Push(S, p->lchild); // 向左走到尽头
Pop(S, p); // 空指针退栈(叶子的左孩子)
if (!StackEmpty(S))
{ // 访问结点,向右一步
Pop(S, p);
printf("%d",p->data); //当前根结点
Push(S, p->rchild);
}
}
return OK;
}
/*******************************************/
/* 按照中序非递归遍历二叉树 */
/*******************************************/
Status InOrderTraverse(BiTree T)
{
stack S;
InitStack(S);
BiTree p=T;
while (p || !StackEmpty(S))
{
if (p)
{
Push(S, p);
p = p->lchild;
} // 非空指针进栈,继续左进
else
{ // 上层指针退栈,访问其所指结点,再向右进
Pop(S, p);
printf("%d",p->data);
p = p->rchild;
}
}
return OK;
}
//二叉树的后序遍历:
/*******************************************/
/* 按照后序递归遍历二叉树 */
/*******************************************/
Status PostOrderTraverse(BiTree T)
{
if(T)
{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%d",T->data);
}
return OK;
}
/*******************************************/
/* 按照后序非递归遍历二叉树 */
/*******************************************/
Status PostOrderTraverse(BiTree T)
{
stack S;
InitStack(S);
BiTree p=T,pre=NULL;
while ( p || !StackEmpty(S))
{
if (p)
{
Push(S,p);
p = p->left;
}
else
{
Pop(S,p);
if (p->right!=NULL && pre!=p->right)
{ //pre指向上次访问的右结点,避免再次访问
p=p->right;
}
else
{
printf("%d",p->data);
pre=p;
p=NULL;
}
}
}
}
/*******************************************/
/* 按照后序非递归遍历二叉树 */
/*******************************************/
Status PostOrderTraverse(BiTree T)
{
BiTree p = T,last = NULL;
stack S;
InitStack(S);
Push(S,p);
while(!StackEmpty(S))
{
Pop(S,p);
if(last == p->left || last == p->right)//左右子树已经访问完了,该访问根节点了
{
printf("%d",p->data);
last = p;
}
else if(p->left || p->right) //左右子树未访问,当前节点入栈,左右节点入栈
{
Push(S,p);
if(p->right)
Push(S,p->right);
if(p->left)
Push(S,p->left);
}
else //当前节点为叶节点,访问
{
printf("%d",p->data);
last = p;
}
}
}
//二叉树的层次遍历:
/*******************************************/
/* 按照层次遍历二叉树 */
/*******************************************/
void LevelOrderTraverse(BiTree T)
{
Queue BiNodeQueue;
BiTree p=T;
EnQueue(BiNodeQueue,p);
while(!BiNodeQueue.Empty())
{
DeQueue(BiNodeQueue,p);
if(p)
{
printf("%c",p->data);
EnQueue(BiNodeQueue,p->lchild);
EnQueue(BiNodeQueue,p->rchild);
}
}
}
//交换左右子树:
/*******************************************/
/* 递归法将二叉树的左右子树互换 */
/*******************************************/
void Exchange(BiTree T)
{
BiTree temp;
if(T)
{
Exchange1(T->lchild);
Exchange1(T->rchild);
temp=T->lchild;
T->lchild=T->rchild;
T->rchild=temp;
}
}
/*******************************************/
/* 非递归法将二叉树的左右子树互换 */
/*******************************************/
void Exchange(BiTree T)
{
stack S;
InitStack(S);
BiTree p=T,temp;
while(p||!StackEmpty(S))
{
if(p)
{
Push(S,p);
temp=p->lchild;
p->lchild=p->rchild;
p->rchild=temp;
p=p->lchild;
}
else
{
Pop(S,p);
p->rchild;
}
}
}
//7.统计二叉树中叶子结点的数目:
/*******************************************/
/* 递归法求叶子结点个数 */
/*******************************************/
int LeavesNum(BiTree T)
{
if(T)
{
if(T->lchild==NULL&&T->rchild==NULL)
{
return 1;
}
return LeavesNum(T->lchild)+LeavesNum(T->rchild);
}
return 0;
}
/*******************************************/
/* 非递归法求叶子结点个数 */
/*******************************************/
int LeavesNum(BiTree T)
{
int count=0;
stack S;
InitStack(S);
BiTree p=T;
while(p||!StackEmpty(S))
{
if(p)
{
Push(S,p);
if(p->lchild==NULL&&p->rchild==NULL)
{
count++;
}
p=p->lchild;
}
else
{
Pop(S,p);
p=p->rchild;
}
}
return count;
}
//8.求二叉树的深度:
/**********************************************/
/* 求一棵树的高度 */
/**********************************************/
int Depth(BiTree T)
{
int lh = rh =0 ;
BiTree p=T;
if(p==NULL)
{
return 0 ;
}
else
{
lh = Depth( p->lchild ) ;
rh = Depth( p->rchild ) ;
return ( lh > rh ? lh : rh ) + 1 ;
}
}
//9.判断两棵树是否等价:
/*******************************************************/
/* 判断两棵是否等价 */
/*******************************************************/
int Is_equal( BiTree T1 , BiTree T2 )
{
int t=0;
if(NULL == T1 && NULL == T2)
{
t=1;
}
else
{
if(NULL !=T1 &&NULL != T2 )
{
if(T1->data == T2->data)
{
if(Is_equal(T1->lchild,T2->lchild))
{
t=Is_equal(T1->rchild,T2->rchild);
}
}
}
}
return t;
}
//10.查找某个信息是否在这棵树中
/****************************************************/
/* 查找某个信息是否在这棵树中 */
/****************************************************/
BiTree Locate(BiTree T,char x)
{
BiTree p=T;
if(P==NULL)
return NULL;
else
{
if( P -> data == x )
return P;
else
{
p = Locate(P->lchild,x);
if(p)
return p;
else
return Locate(P->rchild,x);
}
}
}
//11.结点个数:
/****************************************************/
/* 树的结点个数 */
/****************************************************/
int Num_Of_Node(BiTree t)
{
if(t==NULL)
return 0 ;
else
return Num_Of_Node(t->lchild)+Num_Of_Node(t->rchild)+1;
}
二叉树,或者说树都是一个递归的概念,他们的左右孩子一样还是二叉树。
在二叉树中,还有完全二叉树和满二叉树的概念
一颗深度为k而且2^k - 1个结点的二叉树称为满二叉树(下图a便是满二叉树)。满二叉树的特点是每一层上的结点数都是最大结点数。
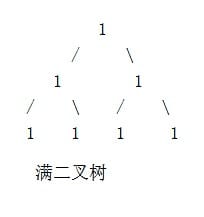
(a)
可以对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左而右。就此,可以引出完全二叉树的定义:
深度为k的,由n个结点的二叉树,当且仅当其每一个结点都与深度为k的慢二叉树中编号1至n的结点一一对应时,称之为完全二叉树(如下图b)。完全二叉树的特点是:

(b)
1.叶子结点只可能在层次最大的两层上出现
2.对任一结点,若其右分支下的子孙的最大层次为L,则其左下分支下的子孙的最大层次必为l或l+1。
一定要区分好满二叉树和完全二叉树。
在性质4、5将用到满二叉树和完全二叉树。
性质
1.在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
2. 深度为k的二叉树至多有2^k - 1个结点(k >= 1)
3.对任何一颗二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1
4.具有n个结点的完全二叉树(其深度为[log2n]+1)的结点按层序编号(从第一层到第[log2n]+1层,每层从左到右),则对任一结点i(11,则其双亲PARENT(i)是结点[i/2]
- 如果2i>n。则结点i无左孩子(结点i为叶子结点);否者其左孩子LCHILD (i)是结点2i
- 如果2i + 1 > n。则结点i无右孩子;否则其右孩子RCHILD(i)是结点2i + 1
(这个性质也方便了二叉树的线性存储)
存储结构
顺序存储结构
存储结构如名,按照顺序存储结构的的定义,用一组地址连续的存储单元依次自上而下,自左至右的存储完全二叉树上的结点元素,即将完全二叉树上的编号为i的结点元素存储在上述定义的一位数组中下标为i-1的分量中。
这种存储结构仅适用于完全二叉树,因为在最坏的情况下,一个深度为k ,且只有k个结点的单支树(树中不存在度为2的结点),却要使用长度为2^k - 1的一位数组。
(线段树就是用的这种存储结构,因为线段树分布比较均匀,虽然不是完全二叉树,)这种存储结构如果在树分布比较均匀的情况下,还是可以使用的,虽然特殊情况有些占用内存,但是操作十分简单,而且静态速度也快。
链式存储结构
要表示二叉树的链表中的结点至少包含3个域:数据域和左右指针域,有时为了方便还需要包含一个指向双亲的指针域。那么利用这两种结点结构所得二叉树的存储结构分别称之为二叉链表和三叉链表。(三叉链表是为了方便寻找双亲结点而存在的,因为在包含n个结点的二叉链表中有n+1个空链域,为方便查找前驱后继,又引入线索链表的概念)。
上面讲的实现就是链式存储结构,这也是二叉树最基本最常用的存储结构。
在以后写树和森林的时候,再又特殊到一般总结树的存储方式。


