当用二叉链表作为二叉树的存储结构时，因为每个结点中只有指向其左、右儿子结点的指针，所以从任一结点出发只能直接找到该结点的左、右儿子。在一般情况下靠它无法直接找到该结点在某种遍历序下的前驱和后继结点。如果在每个结点中增加指向其前驱和后继结点的指针，将降低存储空间的效率。

我们可以证明：在n个结点的二叉链表中含有n+1个空指针。因为含n个结点的二叉链表中含有个指针，除了根结点，每个结点都有一个从父结点指向该结点的指针，因此一共使用了n-1个指针，所以在n个结点的二叉链表中含有n+1个空指针。

因此可以利用这些空指针，存放指向结点在某种遍历次序下的前驱和后继结点的指针。这种附加的指针称为线索，加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树。为了区分一个结点的指针是指向其儿子的指针，还是指向其前驱或后继结点的线索，可在每个结点中增加两个线索标志。这样，线索二叉树结点类型定义为：

type
 TPosition=^thrNodeType;
 thrNodeType=record
              Label:LabelType;
              ltag,rtag:0..1;
              LeftChild,RightChild:TPosition;
             end;

线索二叉树

其中ltag为左线索标志，rtag为右线索标志。它们的含义是:

• ltag=0，LeftChild是指向结点左儿子的指针；
• ltag=1，LeftChild是指向结点前驱的左线索。
• rtag=0，RightChild是指向结点右儿子的指针；
• rtag=1，RihgtChild是指向结点后继的右线索。

例如图(a)是一棵中序线索二叉树，它的线索链表如图(b)所示。

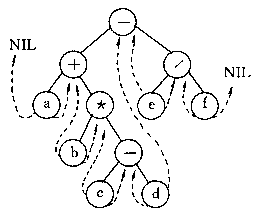
（a）

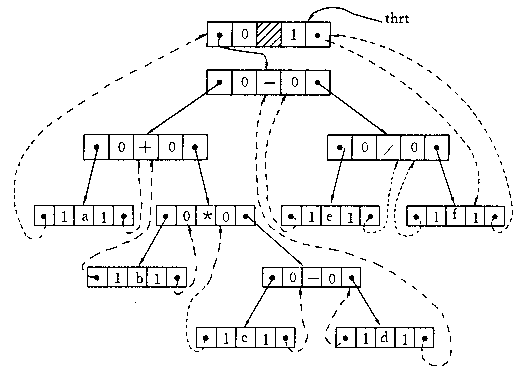
（b）

图(b)中，在二叉树的线索链表上增加了一个头结点，其LeftChild指针指向二叉树的根结点，其RightChild指针指向中序遍历时的最后一个结点。另外，二叉树中依中序列表的第一个结点的LeftChild指针，和最后一个结点的RightChild指针都指向头结点。这就像为二叉树建立了一个双向线索链表，既可从第一个结点起，顺着后继进行遍历，也可从最后一个结点起顺着前驱进行遍历。

如何在线索二叉树中找结点的前驱和后继结点？

以图的中序线索二叉树为例。树中所有叶结点的右链是线索，因此叶结点的RightChild指向该结点的后继结点，如图中结点"b"的后继为结点""。当一个内部结点右线索标志为0时，其RightChild指针指向其右儿子，因此无法由RightChild得到其后继结点。然而，由中序遍历的定义可知，该结点的后继应是遍历其右子树时访问的第一个结点，即右子树中最左下的结点。例如在找结点""的后继时，首先沿右指针找到其右子树的根结点"-"，然后沿其LeftChild指针往下直至其左线索标志为1的结点，即为其后继结点(在图中是结点"c")。类似地，在中序线索树中找结点的前驱结点的规律是：若该结点的左线索标志为1，则LeftChild为线索，直接指向其前驱结点，否则遍历左子树时最后访问的那个结点，即左子树中最右下的结点为其前驱结点。由此可知，若线索二叉树的高度为h，则在最坏情况下，可在O(h)时间内找到一个结点的前驱或后继结点。在对中序线索二叉树进行遍历时，无须像非线索树的遍历那样，利用递归引入栈来保存待访问的子树信息。

对一棵非线索二叉树以某种次序遍历使其变为一棵线索二叉树的过程称为二叉树的线索化。由于线索化的实质是将二叉链表中的空指针改为指向结点前驱或后继的线索，而一个结点的前驱或后继结点的信息只有在遍历时才能得到，因此线索化的过程即为在遍历过程中修改空指针的过程。为了记下遍历过程中访问结点的先后次序，可附设一个指针pre始终指向刚刚访问过的结点。当指针p指向当前访问的结点时，pre指向它的前驱。由此也可推知pre所指结点的后继为p所指的当前结点。这样就可在遍历过程中将二叉树线索化。对于找前驱和后继结点这二种运算而言，线索树优于非线索树。但线索树也有其缺点。在进行插人和删除操作时，线索树比非线索树的时间开销大。原因在于在线索树中进行插人和删除时，除了修改相应的指针外，还要修改相应的线索。

其实线索树是为了快速查询任意结点的前驱和后继而存在的。这也是它的优势。但是，如果删除插入频繁的话，反而不是好的选择。

这篇文章转载自HUST。