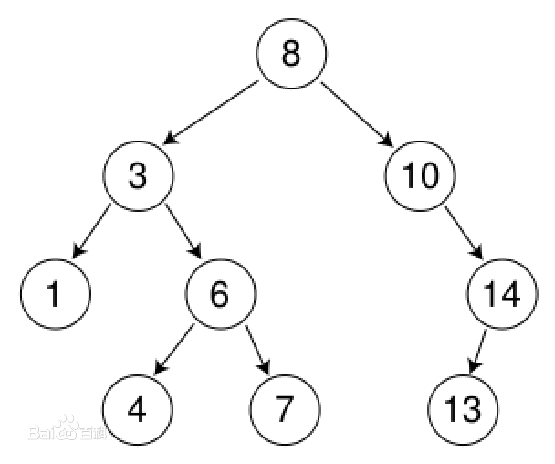
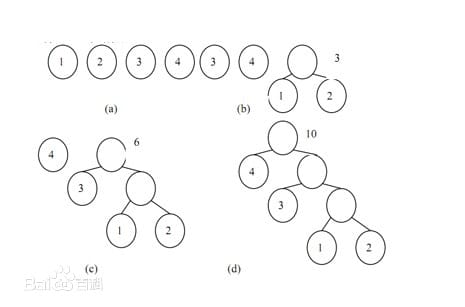
树模型的拓展
树的等价问题
在离散数学中,对等价关系和对价类的定义是: 如果集合S中的关系R是自反的,对称的和传递的,则称它为一个等价关系。 设R是集合S的等价关系。对任何x∈S,由[x]R={y|y∈S∩xRy}给出的集合[x]R⊆S称为由x∈S生成的一个R等价类。 若R是集合S的等价关系。则由这个等价关系可产生这个集合的唯一划分。即可以按R将S划分为若干不相交的子集S1,S2,...,它们的并即为S,则这些子集Si便称为S的R等价类。 应该如何划分等价类呢?假设集合S有n个元素,m个形如(x,y)(x,y∈S)的等价偶对确定了等价关系R,需求S的划分。 确定等价类的算法可如下进行:
- 令S中每个元素各自形成一个单个成员的子集,记做S1,S2,...,Sn。
- 重复读入m个偶对,对每个读入的偶对(x,y),判读x和y所属子集。不失一般性,假设x∈Si,y∈Sj,若Si!=Sj,则将Si并入Sj,并置Si为空(或将Sj并入Si并置Sj为空)。则当m个偶对都被处理之后,S1,S2,...,Sn中所有非空子集即为S的R等价类。
因此,可见划分等价类需对集合进行的操作有3个:其一是构造只含单个成员的集合;其二是判定某个单元素所在子集;其三是归并两个互不相交的集合为一个集合。 以集合为基础的抽象数据类型可用多种实现方法,如用位向量表示集合或用有序表表示集合。 如何高效的实现以集合为基础操作的抽象数据类型,则取决于该集合打大小以及对此集合所进行的操作。 数据结构中引入一个叫MFSet 的ADT,其实他就是并查集(见CSDN博客当时的并查集总结)的完善版 结构存储父结点,当两个结点的祖宗结点相同时便可以认为这是属于同一个集合的结点。 找祖宗操作:
int find_mfset(MFSet S, int i) {
// 找集合S中i所在子集的根
int j;
if (i<0 || i>S.n) return -1; // i不是S中任一子集的成员
if (i==0)
printf("t%d(%d%3d)n",i,S.nodes[0].data,S.nodes[0].parent);
for (j=i; S.nodes[j].parent>=0; j=S.nodes[j].parent)
printf("t%d(%d%3d)n",j,S.nodes[j].data,S.nodes[j].parent);
return 1;
}// find_mfset
两个结点判断是否一个集合:
Status merge_mfset(MFSet &S, int i, int j) {
// S.nodes[i]和S.nodes[j]分别为S中两个互不相交的子集Si和Sj的根结点。
// 求并集Si∪Sj。
if (i<0 || i>S.n || j<0 || j>S.n) return ERROR;
S.nodes[i].parent = j;
return OK;
} // merge_mfset
在使用并查集的时候有个需要注意的地方,就是整个算法的时间复杂度是和树的深度有关的。 如果建的树除了叶子外只有出度为1的结点,这种极端的例子时间复杂度高达O(n^2)。 那么解决个弊端有两个方式,一是选择结点较少的一枝添加结点,顶一个是就是“路径压缩” 路径压缩是在学并查集就学的东西,在集训的时候就已经没有问题,但书中提出了选择建树是一个我没有想到过的优化方式,
Status mix_mfset(MFSet &S, int i, int j) {
// S.nodes[i]和S.nodes[j]分别为S中两个互不相交的子集Si和Sj的根结点
// 求并集Si∪Sj。
if (i<0 || i>S.n || j<0 || j>S.n) return ERROR;
if (S.nodes[i].parent>S.nodes[j].parent) { // Si所含成员数比Sj少
S.nodes[j].parent+=S.nodes[i].parent;
S.nodes[i].parent=j;
} else { // Sj的元素比Si少
S.nodes[i].parent+=S.nodes[j].parent;
S.nodes[j].parent=i;
}
return OK;
} // mix_mfset
这种方式使建的树深度不会超过[log2n]+1。 但是我还是更喜欢路径压缩,一是简单,压缩在查询的过程中完成了,而是压缩完,路经长度不会大于4 只需要修改find查找函数即可以实现:
int fix_mfset(MFSet &S, int i) {
// 确定i所在子集,并将从i至根路径上所有结点都变成根的孩子结点。
int j,k,t;
if (i<1 || i>S.n) return -1; // i 不是S中任一子集的成员
for (j=i; S.nodes[j].parent>=0; j=S.nodes[j].parent)
printf("t%d(%d%3d)n", j, S.nodes[j].data, S.nodes[j].parent);
for (k=i; k!=j; k=t) {
t=S.nodes[k].parent; S.nodes[k].parent=j;
}
return 1;
} // fix_mfset
树的计数
树的计数放在了最后一节,其实到现在证明我也没有看明白,先把结论总结下来吧。
这一节主要讨论的是具有n个结点的不同形态树有多少棵。
二叉树相似是指:二者都为空树或二者均不为空树而且他们的左右子树分别相似
二叉树等价是指:二者不仅相似,而且所有对应结点上的数据元素均相同。
二叉树的计数问题就是讨论二叉具有n个结点、互不相似的二叉树的数目bn。
在n很小的时候,可直观的得到b0=1为空树;b1=1是只有一个根结点树,b2=2,b3=5。
一般情况下,一棵具有n(n>1)个结点的二叉树可以看成是由一个根结点、一棵具有i个结点的左子树和一棵具有n-i-1个结点的左右子树组成,其中0<=i<=n-1由此可得地推公式
b0=1
bn=Σ(n-1,i=0)bi bn-i-1 (n>=1)
最后,前序或后序加上中序遍历就可以确定一棵唯一的树,这也是判断两个树是否相同最好的方式。
树和森林
树的存储
树的各种操作还是离不开树的存储的,其实树的存储才是最好玩的东西。
双亲表示法
假设以一组连续的空间存储树的结点,同时在每个结点中附设一个指示器指示其双亲结点在链表中的位置
#define MAX_TREE_SIZE 100
typedef struct //节点结构
{
TElemType data;
int parent; //双亲位置域
}PTNode;
typedef struct //树结构
{
PTNode node[MAX_TREE_SIZE];
int count; //根的位置和节点个数
}PTree;
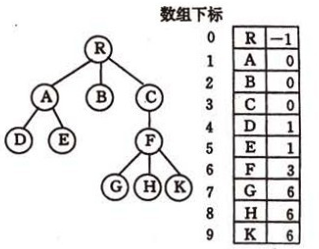
这种存储结构利用了每个结点(除了根结点以外)只有唯一的双亲的性质,在查找双亲的操作中可以在O(1)内实现,对于查找根结点也不过多次找双亲,实现和时间复杂度都可以接受。 但是,如果要找孩子结点,要遍历整棵树!!!因此,数据结构和算法是相互服务的,看需求选择。
孩子表示法
由于每个结点可能有多个子树,则可用多重链表,即每个结点有多个指针域,其中每个指针指向一棵树的根结点。 其实和二叉链表很像,但是不一定是几个叉,也就是说对于孩子指针域,个数不确定,那么我们也要重新考虑这个问题,设定几个指针,既然个数不确定,那用动态存储就比较好,那么,指针域用链表存储,那么实现存储一棵树就应该是这个样子:
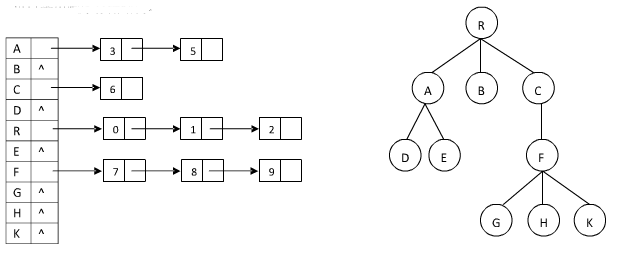
实现虽然麻烦,但是这应该是最直观最好理解的存储方式,不作细总结了。
孩子兄弟表示法
孩子兄弟表示法又称二叉树表示法,或二叉链表表示法。即以二叉链表作树的存储结构。链表中结点的两个链域分表指向该结点的第一个孩子结点和下一个兄弟结点。是不是很炫酷。。。
typedef struct CSNode
{
TElemType data;
CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;
其实就是左支保存孩子,右支保存兄弟,当想遍历所有孩子的时候,只需要先遍历左子树一次,然后遍历左子树的右子树到空就可以了。 如果只看孩子兄弟表示法不形象的话,参照孩子孩子表示法便可以知道存储的是什么样子的:
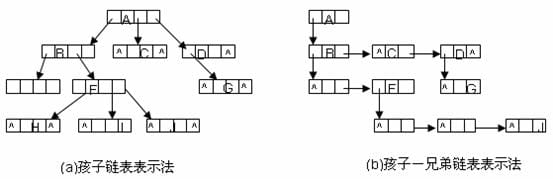
也就是有这样的存储结构,所以树和森林转换起来非常的方便。
森林和二叉树的转换
由于二叉树和树都可以用二叉链表作为存储结构,则以二叉链表作为媒介可导出树和二叉树之间的一个对应关系。也就是说,给定一棵树,可以找到一颗二叉树与之对应,从物理结构来看,它们的二叉链表是相同的,只是解释不同而已。
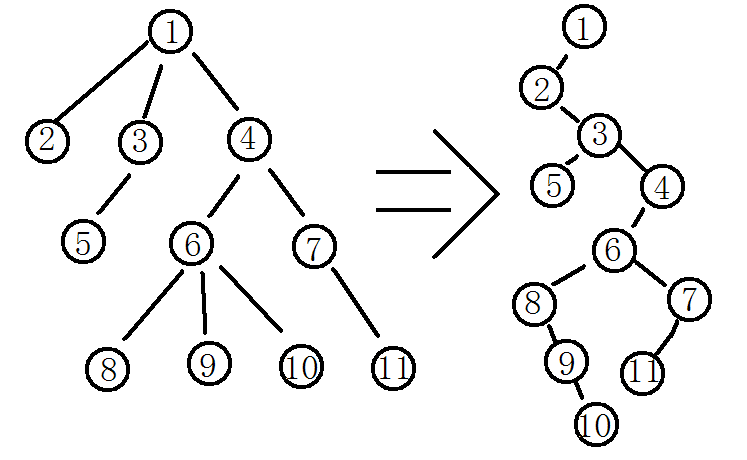
对于右面那棵树,即可以认为他是左面那可树的存储结构表示,也可以认为他本来就是一棵二叉树。 如果按照孩子兄弟表示法,我们可知,根结点的右支必为空(根没有兄弟),那么若把森林中第二棵树的根结点看成是第一棵树的根结点的兄弟,则同样可导出森林和二叉树的对应关系。 这个一一对应的关系导致森林或树与二叉树可以相互转换:
森林转换为二叉树
如果F={T1,T2,...,Tm}是森林,则可按如下规则转换成一棵二叉树B=(root,LB,RB)。
- 若F为空,即m=0,则B为空树
- 若F非空,即m!=0,则B的根root即为森林中第一棵树的根ROOT(T1);B的左子树LB是从T1中根结点的子树森林F1={T11,T12,....,T1m1}转换而成的二叉树,其右子树RB是从森林F'={T2,T3,...,Tm}转换而成的二叉树
二叉树转换为森林
如果B=(root,LB,RB)是一棵二叉树,则可按如下规则转换成森林F={T1,T2,...,Tm}。
- 若B为空,则F为空
- 若B非空,则F中第一棵树T1的根ROOT(T1)即为二叉树B的根root;T1中根结点的子树森林F1是由B的左子树LB转换而成的森林;F中除T1之外其余树组成F'={T2,T3,...,Tm}是由B的右子树RB转换而成的森林。
明显,上述算法为递归算法。
树和森林的遍历
已知二叉树有三种遍历方式,因为树和森林都可以用二叉链表,因此树和森林的遍历的实现也算是依靠着树的遍历实现的。 由树结构的定义可引出两种次序遍历树的方法,一种是先根遍历树,即:先访问树的根结点,然后依次访问先根遍历根的每一棵树;另一种是后根遍历,即:先依次后根遍历每一棵树,然后访问根结点。 按照森林和树的相互递归关系,我们可以推出森林的两种遍历方法:
先序遍历森林
若森林非空,则可按照下述规则遍历之:
- 访问森林第一棵树的根结点
- 先序遍历第一棵树中根结点的子树森林
- 先序遍历除去第一棵树之后剩余的树构成的森林
中序遍历森林
若森林非空,则可按照下述规则遍历之:
- 中序遍历森林中的第一棵树的根结点的子树森林
- 访问第一棵树的根结点
- 中序遍历除去第一棵树之后剩余的树构成的森林
其实说白了,森林的先序和中序遍历分别对应了二叉树的先序和中序遍历(当用孩子兄弟表示法的时候)。
Copyright © 2020 Powered by MWeb, Theme used GitHub CSS.