昨天晚上和RE聊完天之后，单JJ问了我一个二叉排序树问题，那个题目不难，就是给一个了一棵二叉排序树作为模型，有给了若干棵二叉排序树，问这几棵树和模型树是否是同一棵树。这么一个小问题搞了半个小时，简直了。这个题目只需要写一个BST建树函数和求前序和中序的函数（一棵唯一的树有唯一的前中序或中后序），然后对模型树和这若干树进行前中序比较，如果完全相同，就可以判断为同一棵树。 昨天才发现没有写过二叉排序树的建树，也发现《数据结构》木有讲二叉排序树，今天算是总结一些BST问题。

什么BST

二叉排序树（Binary Sort Tree）又称二叉查找树（Binary Search Tree），亦称二叉搜索树。 它或者是一棵空树；或者是具有下列性质的二叉树： （1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值； （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值； （3）左、右子树也分别为二叉排序树； 又是一个递归的定义。

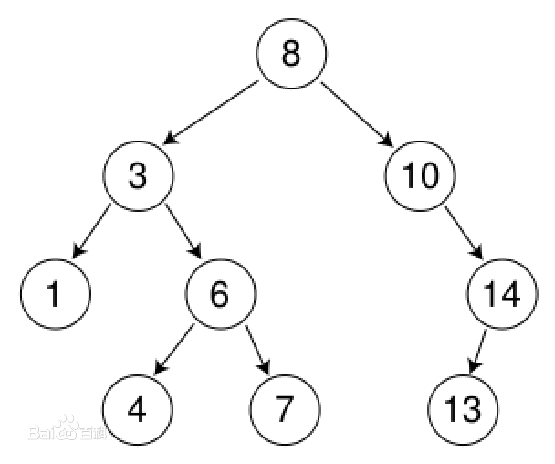
说白了，就是：左孩子的二叉树。 也就是因为BST的特性，导致他在元素查找的时候比普通二叉树更有优势（有点像二分），但整棵树要满足这个性质，也注定让BST在建立和删除的时候和普通二叉树不一样。

BST的插入

BST的插入是建立BST的基础，在插入一棵BST的时候一定要注意满足左

void inst(node *rt,node *root)
{
    if(rt->data data)
    {
        if(root->lc == NULL)
            root->lc = rt;
        inst(rt,root->lc);
    }else
    {
        if(root->rc == NULL)
            root->rc = rt;
        inst(rt,root->rc);
    }
}

建立BST

建立BST是在插入BST的基础上的，因为建立一棵BST的过程就是一个一个将结点插入到树的过程。

node *build(char *s)
{
    node *root = NULL;
    while(*s !='�')
    {
        node *rt = new node;
        rt->data = *(s++);
        rt->lc = NULL;
        rt->rc = NULL;
        if(root == NULL)
            root = rt;
        else
            inst(rt,root);
    }

    return root;
}

BST的查找

BST也被称为二叉查找树的原因就是它的查找优势，二分，在每经过一个结点的时候，可以放弃树的另一枝而不用遍历整棵树。

node *findnode(int data,node *root)
{
    if(root == NULL)
        return NULL;

    if(data == root->data)
        return root;
    else if(data data)
        return findnode(data,root->lc);
    else
        return findnode(data,root->rc);
}

BST的删除

BST的整棵树的删除还是很简单的，一个递归，和删除整个二叉树一样，难的是删除BST的一个结点。

删除整棵树

void deltree(node *root)
{
    if(root == NULL)
        return ;

    deltree(root->lc);
    deltree(root->rc);
    delete(root);
}

 删除结点

删除结点是建立在查找的基础上的，

node *finddlenode(int data,node *root)
{
 if(root)
 {
 if(data == root->data)
 root = delnode(root);
 else if(data data)
 root->lc = finddelnode(data,root->lc);
 else
 root->rc = finddelnode(data,root->rc);
 }

 return root;
}

删除结点，对于BST来讲，就会破坏整棵树的规律，那么当我们删除一个结点之后，可能会遇到4种情况

• 删除的是叶子，还是一棵BST
• 删除的结点只有左孩子
• 删除的结点只有右孩子
• 删除的结点有两个孩子

对于第一种情况，很好办，可以不用考虑，第二种情况以及以后，如果简单考虑，可以认为变成了2-3个BST森林，我们只需要再把它们合成一棵树便好。 对于再把这几棵树合成一棵树，有两种方法（都是利用右枝比根结点大的特殊性） 方法一：

1. 若p有左子树，找到其左子树的最右边的叶子结点r，用该叶子结点r来替代p，把r的左孩子作为r的父亲的右孩子(相当于把r的右枝移上去而把左枝留在原有位置)。
2. 若p没有左子树，直接用p的右孩子取代它。

方法二：

1. 若p有左子树，用p的左孩子取代它；找到其左子树的最右边的叶子结点r，把p的右子树作为r的右子树。
2. 若p没有左子树，直接用p的右孩子取代它。

两种方法都不错，第一种感觉更简单些。 第一种代码

node * delNode(node *root)
{
    node *rnt;
      if (root->lc)
      {
        node *rt = root->lc;   //rt指向其左子树;
        while(rt->rc != NULL)//搜索左子树的最右边的叶子结点rt
        {
            rt = rt->rc;
        }
            rt->rc = root->rc;

            rnt = root->lc;   //rnt指向其左子树;
      }
      else
      {
            rnt = root->rc;   //rnt指向其右子树;
      }
    delete(root);
    return rnt;
}