Copyright © 2020 Powered by MWeb, Theme used GitHub CSS.
C++通过改进C语言,使得应用更容易,最重要的OOP特性:
为了把他们组合在一起,C++所做的最重要的改进是提供了类。
未开发一个类并编写一个使用它的程序,通常,C++程序员将结构(类定义)放在头文件中,并将实现(类方法的代码)放在源代码文件中。
为了帮助识别类,常见但不通用的约定,将类名首字母大写。
类中包含private,public和protected。
类设计尽可能将共有接口与实现细节分开。公有接口表示设计的抽象组件。将实现细节放在一起并将它们与抽象分开被称为封装。数据的隐藏(将数据放在类的私有部分中)是一种封装,将实现的细节隐藏在私有部分中。封装的另一个例子是,将类函数定义和类声明放在不同的文件中。
数据隐藏不仅可以防止直接访问数据,还让开发者无需了解数据是如何被表示的。在对后期程序修改的时候,无需修改程序接口,这使程序维护起来更容易。
由于隐藏数据是OOP主要目标之一,因此数据项通常放在私有部分,组成类接口的成员函数放在公有部分。通常程序员使用私有成员函数来处理不属于公有接口的实现细节。
其实类和结构唯一区别就是结构默认的访问类型是public,而类为private。
除了类的描述(class部分),还需要创建类描述的第二部分:为那些由类声明中的原型表示的成员函数提供代码。成员函数定义与常规函数非常相似,它们有函数头和函数体等等。但是:
定义在类声明中的函数会自动生成内联函数,当然在类声明之外定义的成员函数,也可以使用inline使之成为内联函数。
所创建的每个新的对象都有自己的存储空间,用于存储其内部变量和成员。但同一个类的所有对象共享同一组类方法。在OOP中,调用成员函数被称为发送消息,因此将同样的消息发送给两个不同的对象将调用同一个方法,但该方法被用于两个不同的对象。
C++的目标是使得使用类与使用基本的内置类型(int等)尽可能相同。要创建类对象,可以声明类变量,也可以使用new对类对象分配存储空间。可以将对象作为函数的参数和返回值,也可以将一个对象赋值给另一个。C++提供了一些工具可用于初始化对象,让cin和cout识别对象,甚至在相似的类对象之间进行自动类型转换。
OOP程序员常依照客户/服务器模型进行讨论程序设计,客户是使用类的程序。类声明(包括类方法)构成了服务器,服务器的责任是确保服务器根据该接口可靠并准确地执行。服务器设计人员只能修改类设计的细节而不能修改端口。这样对服务器的修改不会客户的行为造成意外的影响。
C++提供了一个特殊的成员函数——类构造函数,专门用于构造新对象、将值付给他们的数据成员。更准确地说,C++为这些成员函数提供了名称和使用语法,而程序员需要提供方法定义。
构造函数名称与类名相同,注意好参数列表,可以重载。
注意参数名不要和private数据名相同(否则无法赋值),一般采取加前缀的方式。
使用构造函数一般有两种方式,一是显式使用(直接调用构造函数,用好参数),另一种是隐式使用。
class S
{
...
}
//显式使用
S a = S(...);
//隐式使用
s a(...);
//使用new
S *p = new S(...);
若未提供显式初始化值会调用默认构造函数,但不会初始化其成员。
如果没有自定义默认构造函数,编译器会提供一个没有任何操作的默认构造函数。
定义默认构造函数有两种,一是给已有构造函数的所有参数提供默认值;二是通过函数重载定义另一个没有参数的构造函数。
因为只能有一个默认构造函数,因此不要同时出现以上两种方式。用户自定义默认构造函数,一般是给所有成员初始化><。
隐式使用默认构造函数时不要使用括号,画色添足,成声明一个函数了。
在构造函数创建对象后,程序负责跟踪该对象,直到过期为止。
对象过期之后,程序将调用死神函数析构函数。析构函数完成清理工作。其实只有在动态内存上,析构函数才有更实际的意义。
比如,同new开辟的内存,析构函数用delete来释放,其他情况,基本用不到析构函数= =,说的好不负责任。。。。
析构函数和构造函数差不多,只不过前面加了一个~。如果没有手动申明一个析构函数的话,编译器会自动加上析构函数,当然,里面什么都没有,如果自定义类没有涉及到动态内存的话,其实这样也挺好。手懒的表现。
什么时候调用析构函数是由编译器决定的,一般是和栈一样,先入后出。
C++11的初始化列表一样可以用在对象的初始化上,不过列表里的内容是某构造函数的参数列表。
对于类方法不会修改到被调用对象时,应该在函数后面添加const。const能用就用, 不只是安全!
因为在类方法中,终会遇到需要返回或者比较调用对象的信息,那么this指针应时而生,他就是一个指针,指向了当前的调用对象,用法和指针一样。
C++目的就是使得程序员自定义构造的类可以和既有的数据类型使用,因此,可以用对象创建数组等稍微高级点的数据结构。对象数组的初始化方式有点类似结构体,但是花括号内是调用构造函数(显示调用)或者直接什么都不写,默认构造函数构造。(如果是C++11的话,可以直接用初始化列表,这样更像结构体数组了)。
C++自从有了类,就有了一种特殊的作用域。类内的元素,作用域只在类内,也就是说只对类内可见。这就是为什么在定义成员函数时必须使用作用域解析运算符。
因为有了作用域,也就有了作用域为类的常量,如果想用一个const常量来控制数组的长度,这是行不通的,因为在类中声明的const常量要在编译时就要分配空间,而建立类的时候,只是描述这个类而没有分配空间,所以常量的值是未知的,则数组的长度也是未知的。
解决方法有两个,一个是用枚举,一个是用static const,全局常量。
类很适合描述ADT,公有成员函数接口提供了ADT描述的服务,类的私有部分和类方法的代码提供了实现,这些实现对类的客户隐藏。
看书啊看书啊看书啊!
买了小大白书的kindle版,所以用稍微零碎的时间来看小白书,其实一直在说要看完白书啊看完白书啊,其实一批了木有看完。当然,小白对于这个阶段意义不是太大了,把语言篇直接pase,从算法篇开始,再过一遍。
其实看书是个很快的过程,理解用的时间也不是太多,更多的时间是花在总结上,我发现我自从建了博客写学习总结,一个学习过程有1/3是看书理解,1/3是琢磨写总结。几乎和再看一遍用的时间一样。记得开始的时候写数据结构总结,一章就是两三小时。
其实还是很纠结要不要再用这么多时间写总结的,那些不写总结的家伙,看书就是快。都无奈了。
大数问题是进集训队第一周狂刷的东西,挺练模拟能力的,不过今天我才发现白书是用结构体和运算符重载把大数搞定的,我便模仿一下,不用结构体,直接用类,写个大数类,以后直接当模板。
大数,就是特别大的数,因为,大到longlong存储不下去,便需要用数组存储,因此,需要用数组来模拟加减乘除,这次我只打算搞加减乘。
要有长度,保存大数的长度,在计算,打印,都很有必要
要有负号标记,在处理的时候,知道这是一个大负数
一个长数组,用来保存大整数
class bign
{
private:
bool sign;
int len;
int num[MAX_LEN];
}
要有初始化,赋值,包括字符串赋值,int赋值等,本来想和白书一样重载=运算符,但是突然发现我这是在写一个类啊,不是结构体,那么直接重载构造函数就可以了,所以写了无参数,字符串参数,整型参数的构造函数。
可以打印,直接友元函数重载
class bign
{
public:
bign(){len = 0;memset(num,0,sizeof(num));}
bign(char *s)
{
sign = 0;
int s_len = strlen(s);
memset(num,0,sizeof(num));
if(s[0] == '-')
{
sign = 1;
int i = 0;
len = s_len - 1;
for(char *p = s + s_len - 1;p > s;p--)
num[i++] = *p - '0';
}else
{
int i = 0;
len = s_len;
for(char *p = s + s_len - 1;p >= s;p--)
num[i++] = *p - '0';
}
}
bign(int n)
{
len = 0;
sign = 0;
memset(num,0,sizeof(num));
if(n == 0)
{
len = 1;
}else
{
if(n < 0)
{
sign = 1;
n = -n;
}
while(n != 0)
{
num[len++] = n % 10;
n /= 10;
}
}
}
friend ostream& operator << (ostream& os,bign n)
{
if(n.sign)
os << '-';
for(int i = n.len - 1;i >= 0;i--)
os << n.num[i];
return os;
}
};
在设计这些运算之前,我先搞定大数比较的问题,其实是想在大数减法上偷偷懒神马的。
//大数比较
bool operator < (const Bigint & b) const
{
if(sign == b.sign)
{
if((!sign && !b.sign)&&len != b.len) return len < b.len;
if((sign && b.sign)&&len != b.len) return len > b.len;
if(sign)
{
for(int i = len - 1;i >= 0;i--)
if(num[i] != b.num[i]) return num[i] > b.num[i];
}else
{
for(int i = len - 1;i >= 0;i--)
if(num[i] != b.num[i]) return num[i] < b.num[i];
}
}else
{
if(!sign && b.sign) return false;
if(sign && !b.sign) return true;
}
return false;
}
只需要写出一个小余,其他的操作都可以用小余来进行判断。
bool operator > (const Bigint & b) const{return b < *this;}
bool operator <= (const Bigint & b) const{return !(b < *this);}
bool operator >= (const Bigint & b) const{return !(*this < b);}
bool operator != (const Bigint & b) const{return b < *this || *this < b;}
bool operator == (const Bigint & b) const{return !(b < *this) || !(*this < b);}
只为在减法的时候偷偷懒。
在进行加法的时候进行了符号判断,虽然有点感觉是在画蛇添足,但是为了圆这个ADT式的谎,还是加上吧。
//加法
bign operator + (const bign &b) const
{
bign c;
//判断加后符号
if(sign && b.sign)
c.sign = 1;
else if(!sign && b.sign)
return c = b - *this;
else if(sign && !b.sign)
return c = *this - b;
c.len = 0;
for(int i = 0,g = 0;g || i < max(len,b.len);i++)
{
int x = g;
if(i < len) x += num[i];
if(i < b.len) x += b.num[i];
c.num[c.len++] = x % 10;
g = x / 10;
}
return c;
}
bign operator += (const bign &b)
{
*this = *this + b;
return *this;
}
有了大数比较之后,就可以轻松的偷懒了。
//减法
Bigint operator - (const Bigint &b) const
{
Bigint c;
c.len = 0;
if(*this > b)
{
c.sign = 0;
for(int i = 0;i < max(len,b.len);i++)
{
int x = 0;
if(i < len) x += num[i];
if(i < b.len) x -= b.num[i];
if(c.len > 0 && c.num[c.len - 1] < 0){c.num[c.len - 1] += 10;x--;}
c.num[c.len++] = x;
}
}else if(*this < b)
{
c.sign = 1;
for(int i = 0;i < max(len,b.len);i++)
{
int x = 0;
if(i < len) x -= num[i];
if(i < b.len) x += b.num[i];
if(c.len > 0 && c.num[c.len - 1] < 0){c.num[c.len - 1] += 10;x--;}
c.num[c.len++] = x;
}
}else
{
c = 0;
}
while(c.num[c.len - 1] == 0 && c.len > 0)
c.len--;
if(c.len == 0) c.len = 1;
return c;
}
Bigint operator -= (const Bigint &b)
{
*this = *this - b;
return *this;
}
在写乘法之前特意去OJ找了两个加法和减法的题目,然后A掉,爽啊,想想还有最后一个乘法,常用大数类就搞出来了,那叫一个激动啊!!!
可以说乘法是比较难搞的,因为时间复杂度有点高。
//乘法
Bigint operator * (const Bigint &b) const
{
Bigint c;
if((sign && b.sign) || (!sign && !b.sign)) c.sign = 0;
else c.sign = 1;
//时间复杂度 O(len * b.len)
for(int i = 0;i < len;i++)
for(int j = 0;j < b.len;j++)
c.num[c.len = max(i + j,c.len),i + j] += num[i] * b.num[j];
for(int i = 0;i < c.len;i++)
if(c.num[i] >= 10) {c.num[i + 1] += c.num[i] / 10;c.num[i] %= 10;}
while(c.num[c.len] != 0)
++c.len;
while(c.num[c.len - 1] == 0 && c.len > 0)
c.len--;
if(c.len == 0) c.len = 1;
return c;
}
Bigint operator *= (const Bigint &b)
{
*this = *this * b;
return *this;
}
到此,常用大数类算是完成了。(除了除法)
#include <iostream>
#include <cstring>
using namespace std;
#define MAX_LEN 1500 //存储大整数的整型数组的长度
class Bigint
{
private:
bool sign;//是否非负数
int len; //长度
int num[MAX_LEN];
public:
Bigint(){len = 0;memset(num,0,sizeof(num));}
Bigint(char *s)
{
sign = 0;
int s_len = strlen(s);
memset(num,0,sizeof(num));
if(s[0] == '-')
{
sign = 1;
int i = 0;
len = s_len - 1;
for(char *p = s + s_len - 1;p > s;p--)
num[i++] = *p - '0';
}else
{
int i = 0;
len = s_len;
for(char *p = s + s_len - 1;p >= s;p--)
num[i++] = *p - '0';
}
}
Bigint(int n)
{
len = 0;
sign = 0;
memset(num,0,sizeof(num));
if(n == 0)//特判
{
len = 1;
}else
{
if(n < 0){sign = 1;n = -n;}
while(n != 0){num[len++] = n % 10;n /= 10;}
}
}
//打印大数
friend ostream& operator << (ostream& os,Bigint &n)
{
if(n.sign)//判断符号
os << '-';
while(n.num[n.len - 1] == 0)
n.len--;
for(int i = n.len - 1;i >= 0;i--)
os << n.num[i];
return os;
}
//大数比较
bool operator < (const Bigint & b) const
{
if(sign == b.sign)
{
if((!sign && !b.sign)&&len != b.len) return len < b.len;
if((sign && b.sign)&&len != b.len) return len > b.len;
if(sign)
{
for(int i = len - 1;i >= 0;i--)
if(num[i] != b.num[i]) return num[i] > b.num[i];
}else
{
for(int i = len - 1;i >= 0;i--)
if(num[i] != b.num[i]) return num[i] < b.num[i];
}
}else
{
if(!sign && b.sign) return false;
if(sign && !b.sign) return true;
}
return false;
}
bool operator > (const Bigint & b) const{return b < *this;}
bool operator <= (const Bigint & b) const{return !(b < *this);}
bool operator >= (const Bigint & b) const{return !(*this < b);}
bool operator != (const Bigint & b) const{return b < *this || *this < b;}
bool operator == (const Bigint & b) const{return !(b < *this) || !(*this < b);}
//加法
Bigint operator + (const Bigint &b) const
{
Bigint c;
//判断加后符号
if(sign && b.sign)
c.sign = 1;
else if(!sign && b.sign)
return c = *this - b;
else if(sign && !b.sign)
return c = b - *this;
c.len = 0;
for(int i = 0,g = 0;g || i < max(len,b.len);i++)
{
int x = g;
if(i < len) x += num[i];
if(i < b.len) x += b.num[i];
c.num[c.len++] = x % 10;
g = x / 10;
}
return c;
}
Bigint operator += (const Bigint &b)
{
*this = *this + b;
return *this;
}
//减法
Bigint operator - (const Bigint &b) const
{
Bigint c;
c.len = 0;
if(*this > b)
{
c.sign = 0;
for(int i = 0;i < max(len,b.len);i++)
{
int x = 0;
if(i < len) x += num[i];
if(i < b.len) x -= b.num[i];
if(c.len > 0 && c.num[c.len - 1] < 0){c.num[c.len - 1] += 10;x--;}
c.num[c.len++] = x;
}
}else if(*this < b)
{
c.sign = 1;
for(int i = 0;i < max(len,b.len);i++)
{
int x = 0;
if(i < len) x -= num[i];
if(i < b.len) x += b.num[i];
if(c.len > 0 && c.num[c.len - 1] < 0){c.num[c.len - 1] += 10;x--;}
c.num[c.len++] = x;
}
}else
{
c = 0;
}
while(c.num[c.len - 1] == 0 && c.len > 0)
c.len--;
if(c.len == 0) c.len = 1;
return c;
}
Bigint operator -= (const Bigint &b)
{
*this = *this - b;
return *this;
}
//乘法
Bigint operator * (const Bigint &b) const
{
Bigint c;
if((sign && b.sign) || (!sign && !b.sign)) c.sign = 0;
else c.sign = 1;
//时间复杂度 O(len * b.len)
for(int i = 0;i < len;i++)
for(int j = 0;j < b.len;j++)
c.num[c.len = max(i + j,c.len),i + j] += num[i] * b.num[j];
for(int i = 0;i < c.len;i++)
if(c.num[i] >= 10) {c.num[i + 1] += c.num[i] / 10;c.num[i] %= 10;}
while(c.num[c.len] != 0)
++c.len;
while(c.num[c.len - 1] == 0 && c.len > 0)
c.len--;
if(c.len == 0) c.len = 1;
return c;
}
Bigint operator *= (const Bigint &b)
{
*this = *this * b;
return *this;
}
//除法
Bigint operator / (const long long b) const
{
Bigint c;
c.sign = 0;
long long n[MAX_LEN];
long long n_len = 0;
long long yushu = 0;
int tf = 0;
for(int i = len;i >= 0;i--)
{
if((yushu * 10 + num[i]) / b)
{
tf = 1;
n[n_len++] = (yushu * 10 + num[i]) / b;
yushu = (yushu * 10 + num[i]) % b;
}else
{
if(tf)
n[n_len++] = 0;
yushu = yushu * 10 + num[i];
}
}
c.len = n_len;
for(int i = 0;i < n_len;i++)
{
c.num[i] = n[n_len - 1 - i];
}
if(c.len == 0)
c.len = 1;
return c;
}
Bigint operator /= (const long long &b)
{
*this = *this / b;
return *this;
}
//取余
long long operator % (const long long b) const
{
long long yushu = 0;
for(int i = len;i >= 0;i--)
{
if((yushu * 10 + num[i]) / b)
{
yushu = (yushu * 10 + num[i]) % b;
}else
{
yushu = yushu * 10 + num[i];
}
}
return yushu;
}
Bigint operator %= (const long long &b)
{
*this = *this % b;
return *this;
}
};
终于看到和图论有关的东西了,这次只是整理《数据结构》的图的知识,等C++过完,看《图论算法理论实现及应用》,再详细深入图论吧。 图是一种较线性表和树更为复杂的数据结构。不同线性表一对一的关系,图表示的多对多的关系。
在图中的数据元素通常称作顶点
VR是两个顶点之间的关系的集合。若<v,w>属于VR,则<v,w>表示从v到w的一条弧,且称v为弧尾或初始点,称w为弧头或终端点,此时的图称为有向图,若<v,w>属于VR必有<w,v>属于VR,即VR是对称的,则以无序对(v,w)代替这两个有序对,表示v和w之间的一条边,此时的图称为无向图。
若<vi,vj>属于VR,则vi!=vj,那么,对于无向图,e的取值范围是0到(n(n-1))/2。有(n(n-1))/2条边的无向图成为完全图。
对于有向图,e的取值范围是0到n(n-1)。具有n(n-1)条弧的有向图称为有向完全图。
又很少条边或弧的图成为稀疏图,反之称为稠密图。
有时图的边或弧具有与它相关的数,这种与图的边或弧相关的数叫做权。这种带权的图通常称为网。
假设有两个图G=(V,{E})和G'=(V',{E'}),如果V'属于V且E'属于E,则称G'为G 的子图。
对于无向图G=(V,{E}),如果边(v,v')属于E,则称顶点v和v'互为邻接点,即v和v'相邻接。边(v,v')依附于顶点v和v',或者说(v,v')与顶点v和v'相关联。
顶点v的度和v相关联的边的数目记为TD(V)。对于有向图G=(V,{A}),如果弧(v,v')属于A,则称顶点v邻接到顶点为v',顶点v'邻接自顶点v。弧<v,v'>和顶点v,v'相关联。以顶点v为头的弧的数目称为v的入度,记为ID(v);以v为尾的弧的数目称为v的出度,记为OD(v);顶点的度为TD(v)=ID(v)+OD(v)。第一个顶点和最后一个顶点相同的路经称为回路或环。
序列中顶点不重复出现的路经称为简单路经。
除了第一个顶点和最后一个顶点之外,其余顶点之外,其余顶点不重复出现的回路称为简单回路或简单环。
在无向图G中,如果从顶点v到顶点v'有路径,则称v和v'是连通的。
对于图中任意两点是连通的,则称图为连通图。
连通分量指的是无向图中的极大连通子图。
在有向图G中,如果对于每一对vi,vj属于V,vi!=vj,从vi到vj和vj到vi都存在路经,则称为强连通图。
有向图的极大强连通子图称作有向图的强连通分量。
一个连通图的生成树是一个极小连通子图。
一棵有向图的生成森林有若干棵有向树组成。
昨天晚上和RE聊完天之后,单JJ问了我一个二叉排序树问题,那个题目不难,就是给一个了一棵二叉排序树作为模型,有给了若干棵二叉排序树,问这几棵树和模型树是否是同一棵树。这么一个小问题搞了半个小时,简直了。这个题目只需要写一个BST建树函数和求前序和中序的函数(一棵唯一的树有唯一的前中序或中后序),然后对模型树和这若干树进行前中序比较,如果完全相同,就可以判断为同一棵树。 昨天才发现没有写过二叉排序树的建树,也发现《数据结构》木有讲二叉排序树,今天算是总结一些BST问题。
二叉排序树(Binary Sort Tree)又称二叉查找树(Binary Search Tree),亦称二叉搜索树。 它或者是一棵空树;或者是具有下列性质的二叉树: (1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值; (2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值; (3)左、右子树也分别为二叉排序树; 又是一个递归的定义。
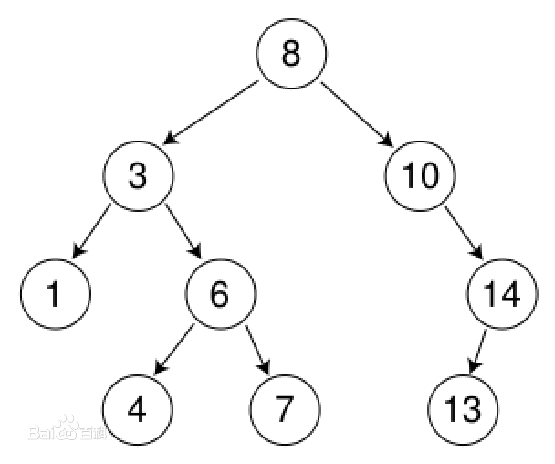
说白了,就是:左孩子的二叉树。 也就是因为BST的特性,导致他在元素查找的时候比普通二叉树更有优势(有点像二分),但整棵树要满足这个性质,也注定让BST在建立和删除的时候和普通二叉树不一样。
BST的插入是建立BST的基础,在插入一棵BST的时候一定要注意满足左
void inst(node *rt,node *root)
{
if(rt->data data)
{
if(root->lc == NULL)
root->lc = rt;
inst(rt,root->lc);
}else
{
if(root->rc == NULL)
root->rc = rt;
inst(rt,root->rc);
}
}
建立BST是在插入BST的基础上的,因为建立一棵BST的过程就是一个一个将结点插入到树的过程。
node *build(char *s)
{
node *root = NULL;
while(*s !='�')
{
node *rt = new node;
rt->data = *(s++);
rt->lc = NULL;
rt->rc = NULL;
if(root == NULL)
root = rt;
else
inst(rt,root);
}
return root;
}
BST也被称为二叉查找树的原因就是它的查找优势,二分,在每经过一个结点的时候,可以放弃树的另一枝而不用遍历整棵树。
node *findnode(int data,node *root)
{
if(root == NULL)
return NULL;
if(data == root->data)
return root;
else if(data data)
return findnode(data,root->lc);
else
return findnode(data,root->rc);
}
BST的整棵树的删除还是很简单的,一个递归,和删除整个二叉树一样,难的是删除BST的一个结点。
void deltree(node *root)
{
if(root == NULL)
return ;
deltree(root->lc);
deltree(root->rc);
delete(root);
}
删除结点是建立在查找的基础上的,
node *finddlenode(int data,node *root)
{
if(root)
{
if(data == root->data)
root = delnode(root);
else if(data data)
root->lc = finddelnode(data,root->lc);
else
root->rc = finddelnode(data,root->rc);
}
return root;
}
删除结点,对于BST来讲,就会破坏整棵树的规律,那么当我们删除一个结点之后,可能会遇到4种情况
对于第一种情况,很好办,可以不用考虑,第二种情况以及以后,如果简单考虑,可以认为变成了2-3个BST森林,我们只需要再把它们合成一棵树便好。 对于再把这几棵树合成一棵树,有两种方法(都是利用右枝比根结点大的特殊性) 方法一:
方法二:
两种方法都不错,第一种感觉更简单些。 第一种代码
node * delNode(node *root)
{
node *rnt;
if (root->lc)
{
node *rt = root->lc; //rt指向其左子树;
while(rt->rc != NULL)//搜索左子树的最右边的叶子结点rt
{
rt = rt->rc;
}
rt->rc = root->rc;
rnt = root->lc; //rnt指向其左子树;
}
else
{
rnt = root->rc; //rnt指向其右子树;
}
delete(root);
return rnt;
}
和C一样,C++为内存存储数据方面提供了多种选择,可以选择数据保留在内存中的时间(生命域)以及程序的哪一部分可以访问数据(作用域和链接)等。
和C语言一样,C++也允许甚至鼓励程序员将组件函数放在独立的文件中。可以单独编译这些文件然后将他们链接成可执行的程序。(IDE包含编译器和链接器的原由吧)。
头文件:包含结构声明和使用这些结构的函数的原型
源代码文件:包含与结构有关的函数的代码
源代码文件:包含调用与结构相关的函数代码
不要将函数定义或变量声明放在头文件中,对于简单的情况是可行的,但是如果存在重复包含头文件的文件,则会出现一个程序中将包含同一个函数的两个定义,除非函数式内联的,否则这将出错。
头文件经常包含的内容:
将结构声明放在头文件中是可以的,因为它们不创建变量,而只是在源代码文件中声明结构变量时,告诉编译器如何创建该结构变量。同样,模板声明不是将被编译的代码,它们指示编译器如何生成与源代码中函数调用相匹配的函数定义。被声明为const的数据和内联函数有特殊的链接属性,因此可以放在头文件。
在C++11中,有四种不同的方案来存储数据,这些方案的区别在于数据保留在内存中的时间。
作用域描述了名称在文件的多大范围内可见。
作用域为局部的变量只在定义它的代码块中可用。代码块是由花括号括起来的一系列语句。作用域为全局(也叫做文件作用域)的变量在定义位置到文件结尾之间都可用。自动变量的作用域为局部,静态变量的作用域是全局还是局部取决于是如何定义的:
链结性描述了名称如何在不同单元间共享:外部链接在文件间共享,内部链接只能有一个文件中的函数共享,自动变量没有链结性,因为它们不能被共享。
mutable说明符指出,即使结构变量为const,其某个成员也可以被修改
struct data
{
char name[30];
mutable int accesses;
...
};
又是一个神器。。
new支持定位操作,
char s[100];
int *p = new(s) int[10];
便可以在s的空间中申明出一个10个元素的int数组。神奇。
但是,因为毕竟不是在堆中开的内存,用delete会错误!
在C++中,名称可以是变量、函数、结构、枚举、类以及类和结构的成员。当随着项目的增大,名称相互冲突的可能性增大。使用多个厂商的类库时,可能导致名称冲突。因此有了名称空间。
传统的C++名称空间,
声明区域是可以在其中声明的区域比如函数外的全局变量。
潜在作用域,变量在潜在作用域从声明点开始,到其声明区域结尾,因此潜在作用域比声明区域小,这是由于变量必须定以后才能使用。
一个名称空间不会和另外一个名称空间冲突。
名称空间可以是全局也可以位于另外一个名称空间中,但不能位于代码块中,因此,默认情况下在名称空间中声明的名称的链接性为外部。
名称空间定义起来很简单:
namespace Jill
{
char fetch(){...}
...
}
使用起来也简单,
Jill::fetch();
为了编程简单,于是有了using声明和using编译指令,
using Jill::fetch;
之后这个函数就可以正常使用了,
using namespace Jill;
之后,这个名称空间里的东西就可以正常使用了。
如果就着尽量节省的原则,前者可以节省更多的代码长度,因为没有用到的函数等其他名称空间的东西没被声明定义。
就着安全的原则,推荐使用第一种以避免多名称空间中的名称冲突。
名称空间是可以嵌套的,不过也很简单。
名称空间可以未命名,因为名称空间定义之后,里面的东西就相当于全局变量,但是未命名就限制了此空间内的东西只能在当前文件使用。
名称空间及其用途
总之,名称空间的引入是为了管理项目。

Copyright © 2020 Powered by MWeb, Theme used GitHub CSS.