数据结构因为考试的原因,学习的进度已经远超总结的进度,现在倒也挺好,当自学完一段时间再写总结,总能把握一些东西,温习一些东西。
和树的遍历类似,我们也需要从图中的某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次。这个过程就叫做图的遍历。
图的遍历算法是求解图的连通性问题,拓扑排序和求关键路径等算法的基础。
深度优先搜索
深度优先搜索(DFS)遍历类似于树的先根遍历,是树的先根遍历的推广。
基本思路
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
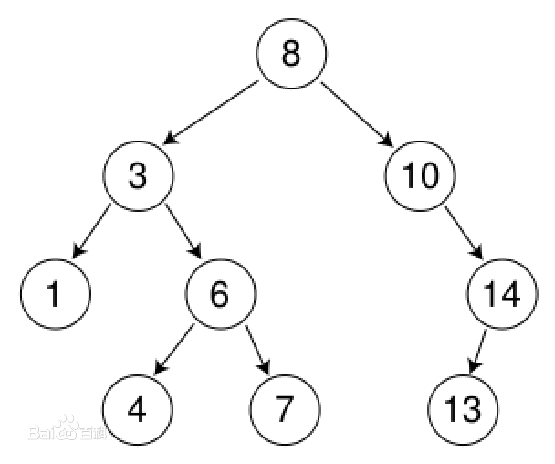
随便那个树做例子(在图中也是一样的),来演示DFS的过程:
首先以8作起点,8好节点入栈(并标记遍历过的节点),然后遍历3号节点,然后3号节点入栈
然后遍历1号节点,并标记。因为1号节点没有后继可以遍历,那么3号节点出栈,回到了了3号节点。
因为3号节点的后继1号节点已经被访问(被标记了),然后就寻找其他后继,发现还有6号节点没有标记(遍历),然后3号节点再次入栈,然后遍历6号节点,6号节点入栈。
6号遍历(标记之后),遍历4号节点,又遇到了没有后继的情况,那么4号节点遍历标记之后6号节点出栈,再次回到6号节点。
又发现6好节点的后继中有7号节点没有遍历,那么6号节点入栈,遍历7号节点。
7号节点没有后继,然后6号节点出栈,回到了3号节点。
3号节点没有可遍历后继,然后3号出栈,回到8号节点,然后发现8号节点有可遍历后继。
以此类推,直到所有节点都没有可遍历后继,那么DFS结束。
伪代码:
void DFSTraverse(Graph G, Status (*Visit)(int v)) {
// 对图G作深度优先遍历。
int v;
VisitFunc = Visit; // 使用全局变量VisitFunc,使DFS不必设函数指针参数
for (v=0; v<G.vexnum; ++v) visited[v] = false; // 访问标志数组初始化
for (v=0; v<G.vexnum; ++v)
if (!visited[v]) DFS(G, v); // 对尚未访问的顶点调用DFS
}
bool visited[MAX_VERTEX_NUM]; // 访问标志数组
Status (* VisitFunc)(int v); // 函数变量
void DFS(Graph G, int v) {
// 从第v个顶点出发递归地深度优先遍历图G。
int w;
visited[v] = true; VisitFunc(v); // 访问第v个顶点
for (w=FirstAdjVex(G, v); w!=-1; w=NextAdjVex(G, v, w))
if (!visited[w]) // 对v的尚未访问的邻接顶点w递归调用DFS
DFS(G, w);
}
遍历图的过程实质上是对每个顶点查找其邻接点的过程。其消耗的时间则取决于所采用的存储结构。当用二维数组表示灵界矩阵作图的存储结构时,查找每个顶点的邻接点所需时间为O(n^2),其中n为图中顶点的个数。而当以邻接表作图的存储结构时,找邻接点所需时间为O(e),其中e为无向图中边的数或有向图中弧的数。由此,当以邻接表作存储结构时,深度优先搜索遍历图的时间复杂度为O(n+e);
广度优先搜索
广度优先搜索(BFS)遍历类似于树的按层次遍历的过程。
自然界的BFS,感觉用这张图片描述算法极其形象!

和DFS相同,BFS也需要一个标记数组,但是不同的是DFS是用栈来实现而BFS是用队列实现。
BFS是树的层次遍历在图的应用,那么再用那个图演示一下BFS。

首先8号节点入队列,现在队列是【8】
然后从队列中拿出第一个元素,开始遍历,把8拿出来,现在队列为空
然后把8号节点标记,表示已经访问过,然后把8号节点所有后继3,10入队列,现在队列是【3,10】。
然后从队列中拿出第一个元素,开始遍历,把3拿出来,现在队列为【10】
然后把3号节点标记,表示已经访问过,然后把3号节点所有后继1,6入队列,现在队列是【10,1,6】。
然后从队列中拿出第一个元素,开始遍历,把10拿出来,现在队列为【1,6】
然后把10号节点标记,表示已经访问过,然后把10号节点所有后继14入队列,现在队列是【1,6,14】。
然后从队列中拿出第一个元素,开始遍历,把拿1出来,现在队列为【6,14】
然后把1号节点标记,表示已经访问过,1号节点没有后继然后不用让任何元素进队列,现在队列是【6,14】。
然后从队列中拿出第一个元素,开始遍历,把6拿出来,现在队列为【14】
然后把6号节点标记,表示已经访问过,然后把6号节点所有后继4,7入队列,现在队列是【14,4,7】。
然后从队列中拿出第一个元素,开始遍历,把14拿出来,现在队列为【4,7】
然后把14号节点标记,表示已经访问过,然后把14号节点所有后继13入队列,现在队列是【4,7,13】。
然后从队列中拿出第一个元素,开始遍历,把4拿出来,现在队列为【7,13】
然后把4号节点标记,表示已经访问过,4号节点没有后继然后不用让任何元素进队列,现在队列是【7,13】。
然后从队列中拿出第一个元素,开始遍历,把7拿出来,现在队列为【13】
然后把7号节点标记,表示已经访问过,7号节点没有后继然后不用让任何元素进队列,现在队列是【13】。
然后从队列中拿出第一个元素,开始遍历,把13拿出来,现在队列为空
然后把13号节点标记,表示已经访问过,13号节点没有后继然后不用让任何元素进队列,现在队列是空。
然后所有成员被访问,BFS结束。
更加上面很啰嗦的描述,我们能发现两点:
- 从第二步开始,算法两步一循环
- 当最后队列为空,说明BFS结束,即所有节点被标记
语言描述什么的不如代码来的直观:
void BFSTraverse(Graph G, Status (*Visit)(int v )) {
// 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组visited。
QElemType v,w;
queue Q;
QElemType u;
for (v=0; v=0; w=NextAdjVex(G, u, w))
if (!visited[w]) { // u的尚未访问的邻接顶点w入队列Q
visited[w] = TRUE; Visit(w);
EnQueue(Q, w);
}//if
}//while
}//if
} // BFSTraverse
因为遍历就是把图中的顶点依次访问,因此DFS和BFS时间复杂度相同,只不过是访问顺序不同罢了。(ps`:因为DFS用了递归,因此在实现上会慢于BFS,但是DFS的非递归方式将和BFS时间复杂度一样)。


